|
Chapter 4
Assembly Language Applied To Game Design
The words, Machine language and/or Assembly language, evoke visions of
indecipherable code to the novice BASIC programmer. The code looks
unfamiliar. But so was BASIC when you were first learning it. While BASIC
has its roots in the English Language and algebraic expressions, Assembly
language appears to consist of unfamiliar op codes or mnemonics that are
used in conjunction with an unfamiliar base 16 number system called
hexadecimal.
It is our intent in this chapter to teach you the fundamentals of
Assembly language programming by comparing it to similar code written in
BASIC. Rather than teach you all aspects of the language, we will
concentrate only on the operations needed to do simple game graphics.
A good Assembler is needed to write Assembly language programs. An
assembler merely translates mnemonics like JMP, which is equivalent to a
GOTO, into hexadecimal opcodes that the computer understands. Most
Assemblers have an editor, an Assembler, and a debugger. The editor allows
you to enter Assembly language code usually by line number and later edit,
delete, or insert particular lines. The Assembler portion converts your
source listing into Machine Code in a two-pass operation. Since any line
of code can have a label in its first field, the Assembler will
automatically calculate the branches or GOTOs to lines referenced with
these labels. Also, if you want to store a variable called ZAP, the
Assembler which assigns a memory storage location for the variable will
automatically furnish the correct memory address for any subsequent store
or load operations using that variable. Last, there is a Machine language
monitor or debugger that helps locate errors. It allows you to examine and
change both memory and internal registers. It also includes step and trace
features that allow you to step through your code one instruction at a
time.
Readers who already own assemblers may use the one they have. We have
provided a translation table in the Appendix in the back of this book to
aid you in converting our SYNASSEMBLER source code to that used in your
assembler. We chose SYNASSEMBLER when we began this book in the Spring of
1983 because it was co-resident (screen editor, assembler, and debugger
are in memory simultaneously) and was available in cartridge form.
For those of you who are new programmers, or are unhappy with their
present assembler, we recommend either the F-S Macro Assembler
40/80 from Stanton Products (See coupon in back of book), an enhanced
disk version of the now discontinued SYNASSEMBLER, or MAC 65
from Optimized Systems Software. Both of these assemblers are fast (2000
lines/minute), are co-resident assemblers, allow source files to be
chained, and offer a choice of assembling to either disk or memory. Both
of these are professional packages and are used as development tools in
various software houses. The F-S Macro Assembler 40/80 and the
discontinued SYNASSEMBLER are both derived from the S-C family of
assemblers on the Apple II computer. Whereas the new F-S Macro Assembler
40/80 is compatible with the new XL series of computers, unpatched
versions of SYNASSEMBLER are not. The F-S Macro Assembler 40/80 is
completely compatible with SYNASSEMBLER source files with the exception of
the way it handles ATASCII string data. A simple global replace will
suffice. (see note in Appendix on assemblers differences.)
Our readers will certainly want to know why we don't use the more
popular Atari Editor Assembler cartridge. First, it is very, very
slow, often taking ten minutes to assemble a 1000 line program. Second, it
doesn't allow chaining of files, nor assembly to the disk. Third, it is
full of bugs. It remains popular mostly to beginner programmers who want
to try to write a very short Assembly language subroutine that will
interface to their BASIC programs.
Basic Assembly Language
The Atari computers contain a central processing unit (CPU), a 6502A
microprocessor that operates at 1. 8 Mhz. It accepts instructions to
perform various operations, like taking a value and storing it somewhere
in memory, adding a number to another number located in one of its
internal registers, or comparing two values. What makes programming in
Assembly language rather difficult (or at least tedious) is that the
computer can only execute one tiny instruction at a time, and only perform
its operations in three internal registers. These three addressable
registers are known as the X register, Y register, and Accumulator. Each
can hold eight binary digits called bits, which are individually valued at
0 or 1. The eight bits, collectively called a byte, have values ranging
from 0 to 255 decimal or ($00 to $FF in hexadecimal notation).
Essentially, the computer, which is an eight-bit microprocessor, can
manipulate data whose values range from all eight bits off (00000000) to
all eight bits on (11111111). The average person has great difficulty in
thinking of values represented by 0's and 1's. Fortunately, someone
invented a number system called hexadecimal, which is base 16 instead of
binary or base 2.
Hexadecimal Numbers
Since 16 is 2x2x2x2, we can divide our eight bits into two four-bit
groups. If you determine each of the decimal equivalents of all the
combinations of base two representations, you obtain the following table.
These values range from 0 to 15 decimal. In the hexadecimal numbering
system, values above 9 are represented by the letters A-F. In order to
prevent confusion between decimal and hexadecimal numbers, hexadecimal
numbers are preceded by a "$". BINARY DECIMAL HEXADECIMAL
0000 0 $0
0001 1 $1
0010 2 $2
0011 3 $3
0100 4 $4
0101 5 $5
0110 6 $6
0111 7 $7
1000 8 $8
1001 9 $9
1010 10 $A
1011 11 $B
1100 12 $C
1101 13 $D
1110 14 $E
1111 15 $F
Hexadecimal numbers are very much like decimal numbers. They can be
added and subtracted in like manner. The only difference is that instead
of having units, tens, hundreds, etc, the hexadecimal numbers have units,
sixteens, 256's, and so forth. Each successive digit is sixteen times the
position to the right instead of ten times as in our decimal system.
DECIMAL HEXADECIMAL
1 6 5 $ 1 3 A
1 HUNDRED 1-256
6 TENS 3 SIXTEENS
6 ONES A-ONES
1 x (100) = 100 1 x (256) = 256
+ 6 x (10) = 60 +3 x ( 16) = 48
+ 5 x( 1) = 5 +A x ( 1) = 10
165 DECIMAL $13A = 312 DECIMAL
Hexadecimal numbers are used to address the Atari's 48000+ memory
locations. Each group of 256 bytes ($00 - $FF) is called a page, starting
with page zero. In 48K Atari computers, memory is directly addressable
from locations $0000 to $BFFF (0 -49151). Locations above $BFFF are also
addressable, but these locations don't contain RAM. The area from $D000 to
$D7FF contain custom hardware chips such as the GTIA, POKEY, PIA, and
ANTIC microprocessor. Some of these hardware locations can be read and
some written to. The area above that, $D800 to $FFFF, contain the 10K
operating system ROMS.
Memory Considerations in Assembly Language
The bottom of RAM, pages 0 thru 5 ($0000 - $05FF) are generally off
limits for program storage. Zero page ($00 - $FF) is a very special area.
There are a number of zero page addressing instructions that execute
faster because they require only two instructions instead of the usual
three. This is because they only need to address a memory location from
$00 to $FF instead of $0000 to $FFFF. These locations are used extensively
by the Operating System.
Only the last few bytes of zero page are available to the user. In
fact, if you are using Synassembler only locations $F0 - $FF are totally
free. You can also use $D6 - $EF, if you don't mind if your data is
altered by the floating point package each time arithmetic operations are
performed by BASIC. And if you are writing a subroutine to be accessed
from BASIC, only locations $CB - $D1 (203-209) are available. $D4 and $D5
can be used to send variables back to BASIC via the USR function.
Page one of memory ($100 - $1FF) is reserved for the stack. It is used
by a special purpose register in the 6502A microprocessor for keeping
track of return addresses when calling subroutines. This scratch area for
the Stack Pointer is sometimes used for temporary register Storage.
Pages two and three are used for various I/0 operations, and operating
system shadow registers, page four for the cassette buffer, page five for
the keyboard buffer, and pages seven through twenty-eight for DOS 2.0's
file management system. Essentially the area below 7420 ($1CFC), with the
exception of page six, is off limits to programmers using DOS. However, if
DOS isn't resident, you can begin storing at 1792 ($700) safely. A pointer
to the low end of memory, MEMLO, can be read at locations 743,744
($2F7,2F8).
Program Counter & Program Status Word
When a microprocessor processes a Machine language program, it keeps
track of which instruction it is executing with an internal 16-bit
register called the program counter. The program counter contains the
current address of the instruction that is being processed. When the
computer finishes with an instruction, it sets a flag or condition in a
7-bit, Program Status Word, which is another register. For example, if you
want to test if a value in the Accumulator is equal to zero, you compare
the value in the Accumulator to zero. If this value is equal to zero, the
zero flag will be set and the next instruction, Branch Equal to Zero
(BEQ), will be executed. Other flags that can be set are the carry flag,
and the negative flag. A diagram of the Program Status Word is shown
below.

OP Codes
The 6502A microprocessor accepts only Machine language instructions.
These are called opcodes. When the computer encounters a $4C, it performs
an equivalent to a GOTO in BASIC. The Machine language instruction $4C 00
08 tells the computer to jump to memory location $800. (Remember,
addresses require two bytes. The low order byte in this case contains $00
and the high order byte, $08--in effect, the reverse order of the actual
values.) Unfortunately, Machine language is difficult to remember, so
programmers invented a substitute called Assembly language, wherein each
opcode is assigned a mnemonic such as JMP, BRK, or LDA. The above example
looks like this: JMP $0800.
If you were to type the following Machine Code into the monitor in your
Assembler, you would see how the monitor disassambler interprets the code,
as in the following example:
4000: A9 30 8D 00 41 CE 00 41 AD 00 41 C9 00 D0 F6 60 [CR]
If you enter a 4000L from the Synassembler monitor you will see the
following: 4000: A9 30 00030 LDA #$30
4002: 8D 00 41 00040 STA $4100
4005: CE 00 41 00050 DEC $4100
4008: AD 00 41 00060 LDA $4100
400B: C9 00 00070 CMP #$00
400D: DO F6 00080 BNE $4005
400F: 60 00090 RTS
The disassembler translates the Machine Code to more easily understood
mnemonics. In the first line of code, LDA is the mnemonic for Load
Accumulator. It is the instruction for the 6502 to load the Accumulator
with an immediate value--in this case, $30. The # sign signifies that it
is an "immediate" instruction; the ($30) is the data portion of the
instruction. The STA in line two is an "absolute" instruction. It
specifies the address in memory for storing the byte of data that is in
the Accumulator.
The difference between "immediate" and "absolute" instructions is an
important point. Let us take the example LDA #$30. In this "immediate"
instruction, the computer takes the operand ($30) as a value and places it
in the Accumulator. However, LDA $30 is an "absolute" instruction, so the
computer takes the operand as an address from which to load data into the
Accumulator. In both cases, we get a value in the Accumulator. You can
tell the modes apart because "immediate" instructions have a # sign before
the operand.
You might wonder, what does this code do? It is a time delay
subroutine. It puts a decimal 48 in memory location $4100. Line two stores
it there, then the value stored at that memory location is decremented by
one in line three. It is then reloaded into the Accumulator to be compared
against the value zero. If it is zero it falls through to the
return-from-subroutine instruction and ends; but if it isn't zero it
branches back to memory location $4005. That location tells the computer
to decrement the value in $4100 once again. The code will perform this
small loop until the value in $4100 becomes zero. At that time, the test
for a zero becomes true and the program returns to the line after the JSR
in the program that called it.
Does it work? First type 400E:00 to change the RTS to a BRK. This
will return us to the monitor when we are finished. Then type 4100:AA
to place something in that memory location so that if you look at it
later you will believe the program did something. Finally, do type 4000G
to start the routine. The code returns you back to the monitor when it
finishes a split second later. Now type 4100 and a 00 is returned.
This is the value in memory location $4100. You can do a 4000S and an
S each time to watch the code single step, or you can trace the entire
operation by typing a 4000T . The strange numbers that appear below
each line of code are the values in the internal registers. A is for
Accumulator, X for X register, Y for Y register, P is the Program Status
Word, and S is the Stack Pointer.
This program has a direct analogy to the following BASIC program: 10 X=48
20 X=X-1
30 IF X<>0 THEN 20
40 RETURN
The major differences between the two programs is that in Assembly
language there are no line numbers used within the code (line numbers are
used only by the editor to place your text in order, and you have to take
care of every minute detail. BASIC automatically assigns the storage
locations of all variables and the location of each instruction in memory.
In Assembly language programming, we have to assign the X variable to
memory location $4100, and have to calculate the relative branch or GOTO
so that it references the memory location $4005. This is done by branching
back $F6 bytes or -8 bytes to the proper address. Yet many of these
details can be greatly simplified if we use an Assembler to do our
programming.
The same program using an Assembler looks like the following: LINE LABEL INSTRUCTION COMMENT
FIELD FIELD FIELD
00010 .OR $4000 ;ASSEMBLE CODE AT $4000
00020 X .EQ $4100 ;X IS STORED AT $4100
00030 LDA #$30
00040 STA X
00050 LOOP DEC X ;X=X-l
00060 LDA X
00070 CMP #$00 ;DONE?
00080 BNE LOOP
00090 RTS
The Assembler generates identical Machine Code, but many of the tedious
details are simplified. Once X is equated to the memory location in line
2, references to that variable in lines 4 through 6 are handled
automatically. If X were assigned to a different memory location because
we lengthened our program, you would only have to change line 2. Also,
labels act like line numbers in BASIC. Since the Assembler assigns the
line of code labeled LOOP to a particular memory location, it can
calculate the correct branch automatically when it encounters line 8
during assembly. The .OR in line 1 is a pseudo-op, understood only by the
Assembler. This does not generate code but tells the Assembler where the
code is to be run and stored. The pseudo-op .TF causes the generated code
to be stored to the disk rather than to memory.
Addressing Modes
Now that you have had a taste of Assembly language programming and have
seen that it isn't as bad as you thought, there are a number of
fundamental operations that must be learned. The most important operation
is to move numbers from one memory location to another. This can be
accomplished by loading a value into any one of three internal 6502
registers--the Accumulator, X, or Y registers--and storing that number
somewhere in memory. A LDA (Load Accumulator) instruction can be carried
out in several different ways depending on its addressing mode. First we
can load the Accumulator with a real hexadecimal value (LDA #$05). This is
called Immediate Mode Addressing. Sometimes we need to be able to load the
Accumulator with a variable stored in a memory location (LDA $4100). This
is called Absolute Addressing.
The only other addressing method that we will discuss for the time
being is the Indexed Addressing mode. It takes the form of LDA $4100,X or
LDA $4100,Y depending on whether the X or Y register is used as an index.
If, for example, the X register contains a #$05, then the instruction
above loads the value from location $4100 + $05 or $4105. This addressing
mode is used primarily for indexing into tables stored at particular
memory locations. There is no problem with the tables crossing page
bounderies. For example, if your table began at $4080 and the X-register
contained a $90, then the instruction LDA $4080,X would fetch the value in
memory location $4080 + $90 or $4110.
EFFECTIVE ADDRESS = ABSOLUTE ADDRESS + X
EFFECTIVE ADDRESS = ABSOLUTE ADDRESS + Y
Store operations are similar to load operations. You can store a value
into an "absolute" memory location, or you can store indirectly into a
memory location, offset by the value contained in either the X or Y
register.
In summary, the table below shows the various load and store
operations.
ACCUMULATOR X REGISTER Y REGISTER
LOAD LDA #$05 LDX #$05 LDY #305
LDA $4100 LDX $4100 LDY $4100
LDA $4100,X LDY $4100,X
LDA $4100,Y LDX $4100,Y
STORE STA $4100 STX $4100 STY $4100
STA $4100,X STY $4100,X *
STA $4100,Y STX $4100,Y *
*Both indirect operations involve zero page addressing only.
Incrementing & Decrementing
Sometimes it is necessary when counting cycles, or looping through code
to increment or decrement a value directly similar to a FOR-NEXT loop in
BASIC. In Assembly language, either the X and Y registers or any memory
location can be incremented or decremented. If the X register contained a
$FE, then it would contain $FF when incremented. But if it contained a
$FF, it would wrap around to become $00. The computer informs you by
setting a zero flag in its Program Status Register. ACCUMULATOR X-REG Y-REG MEMORY LOCATION
INC BY 1 NOT AVAILABLE INX INY INC $4100
DEC BY 1 NOT AVAILABLE DEX DEY DEC $4100
Stack Instructions
There is a special area in the computer ($100 - $1FF) that is used
quite frequently by an internal register called the Stack Pointer. The
computer uses this area to save return addresses when handling either
interrupts or subroutines. The stack is like a dish dispenser. Bytes are
pushed on the stack in order, and pulled off in reverse order. The first
byte stored is the last byte to be pulled off. The Stack Pointer always
points to the next free byte in the stack. Since the stack is only 256
bytes long, only 128 address pairs can be stored at any one time.
Normally the stack would be of little interest to programmers except
that it can also be used to temporarily store data. If you were worried
about your three registers being altered in a subroutine, you could push
all three values onto the stack before calling the subroutine, and then
pull them back off when you return from the subroutine. BASIC also uses
the stack to transfer data in the USR function when calling a Machine
language subroutine. The top byte in the stack contains the number of
variables being passed. The values follow in two byte pairs in hi byte low
byte order.
Two basic Machine language instructions provide key tools for using the
stack. PHA pushes the value in the Accumulator on the Stack. PLA pulls the
top value of the stack and places it in the Accumulator. Since these
instructions only involve the Accumulator, you would need to transfer the
value in the X register to the Accumulator (TXA) in order to save the X
register on the stack. Similarly you would transfer the Y register to the
Accumulator (TYA) first before a PHA to the stack. Be careful when working
with the stack. For instance, if you push data onto the stack while in a
subroutine and don't pull it back off, when the subroutine reaches the RTS
instruction it will return to the main program at the wrong address.
Altering Program Flow
Program flow can be altered, as in BASIC, with instructions that
resemble GOTO, GOSUB, and IF ... THEN statements. The JMP instruction is
equivalent to a GOTO statement; it can transfer control to any location in
the machine to continue executing code. JMP $8D6C instructs the computer
to continue executing code beginning at address $8D6C. The GOSUB statement
is identical to a JSR (jump Subroutine) in Machine language. When the
computer reaches the instruction $5A83, it pushes the two-byte memory
address of the instruction onto the stack, so that when it returns from
the subroutine via an RTS (ReTurn from Subroutine), it will know the
address where it will continue the program. When it returns, it pulls the
return address off the stack and increments it by one so that it points to
the next executable instruction.
The IF ... THEN statement is analogous to a number of branch
instructions which test the Program Status Register to see which flags are
set. Usually, you use compare operations to set flags. You can compare a
value against the value stored in either the Accumulator, the X or the Y
Registers. The mnemonics are CMP, CPX and CPY, respectively. For example, LDA $4100 ;LOAD ACCUMULATOR WITH VALUE AT $4100
CMP #$05
Different flags are set depending on the result.
Branch instructions are very similar to a JMP instruction (which is an
unconditional branch), except that only under certain circumstances will
they cause program flow to continue at a different location. For example,
if we were to test for that wraparound case when we incremented the
X-register that contained $FF, we would want to test the Zero Flag with a
Branch Equal Zero (BEQ) instruction, and go to some label if the condition
is true. LDX $4100 ;LOAD X REGISTER WITH VALUE IN MEMORY
INX ;INCREMENT X - REGISTER
BEQ SKIP ;TEST IF 0, AND IF TRUE GOTO SKIP
RTS ;RETURN TO MAIN PROGRAM
SKIP LDA #$04
. .
. .
This short example loads a value from the memory location into the X
register, then increments it. If wraparound occurs, the test for a zero
flag causes the program to jump to a label called SKIP, and the code does
not return to the program that called it via the RTS. There are numerous
tests on each of the flags in the Program Status Register. A summary is
shown below. BCS - Branch if the carry flag is set. C = 1
BCC - Branch if the carry flag is clear. C = 0
BEQ - Branch if the zero flag is set. Z = 1
BNE - Branch if the zero flag is clear. Z = 0
BMI - Branch if minus. N = 1
BPL - Branch if plus. N = 0
BVS - Branch if overflow is set. V = 1
BVC - Branch if overflow is clear. V = 0
Most Assemblers offer alternative mnemonics for BCC and BCS. Since,
during comparisons, the carry flag is set when the value in the
appropriate register is equal or greater than the value compared, BCS
might be called BGE (Branch Greater or Equal). Likewise, BCC is equivalent
to BLT (Branch Less Than). Why use these alternatives? Because they are
easier to remember and visualize, and they make it clear that you are
doing logical comparisons, rather than testing the results of an addition
or subtraction.
There is one other important concept that should be understood when
doing comparisons. I implied that the subsequent branch was like a GOTO in
BASIC or like a JMP in Assembly language. This is not entirely true, since
the range of the branch cannot exceed -126 to +129 bytes. This is because
the branch instruction is only two bytes long. The first byte is the
instruction code and the second the relative address. It takes a two byte
address to branch to any place in memory (Except Page Zero). The JMP
instruction has the advantage that it is three bytes long. In most cases,
this limitation will not cause problems. But if a "branch out of range
error" occurs, you must reverse the test so that it will reach the
required destination via a JMP instruction.
Example: If BEQ SKIP is out of range then substitute the following: BNE *+$5 or BNE B
JMP SKIP JMP SKIP
. B NOP
. .
This change causes the program to drop through the JMP instruction if
the zero flag was set, and then jump to location SKIP. However, if the
zero flag is not set, it will advance ahead five bytes to the instruction
following the JMP. All other branch instructions work in a similar manner.
This gives the equivalent of a Long Branch.
Addition & Subtraction
Simple addition and subtraction of unsigned numbers is easily
accomplished in Machine language. All additions and subtractions must be
performed one byte at a time. Thus, large numbers or multi-byte numbers
(those that exceed $FF), must be added or subtracted one byte at a time,
and the carry flag must be accounted for. It's actually not much different
from addition of two multi-digit decimal numbers. Those numbers have a
digit in the ones column, another in the tens, etc. If you add 65 to 78,
you add the ones column first. Five plus eight equals 13. The value in the
ones column is 3; you then carry the one "ten" into the tens digit column
before you add the two numbers in the tens column. Hexadecimal addition is
similar. You clear the carry before you add. If the sum of the two values
exceeds $FF, the carry is set. Since you don't clear the carry when adding
the next higher byte, the resultant answer will be the sum plus the
previously computed carry, as in the following example: EXAMPLE: +CARRY
63 F4
+02 +16
--- ---
66 0A ;SETS CARRY
The code for addition and subtractions is as follows:
ADDITIONS
CLC ;CLEAR CARRY
LDA #$F4 ;LOAD LOW ORDER BYTE
ADC #$16 ;ADD WITH CARRY
STA LOW ;STORE LOW BYTE
LDA #$63 ;LOAD HIGH ORDER BYTE
ADC #$02 ;ADD WITH CARRY (NOTE DON'T CLEAR CARRY)
STA HIGH ;STORE HIGH BYTE
SUBTRACTIONS SEC ;SET CARRY FLAG
LDA #$F4 ;LOAD VALUE
SBC #$16 ;SUBTRACT WITH CARRY
STA VALUE ;STORE RESULT
You should be aware that the rules for subtraction are different from
the ones for addition. The carry must be set first. This is equivalent to
a borrow in subtraction. After the subtraction operation, the carry will
be clear if an underflow (borrow) occurred. The carry will be set
otherwise. Setting the carry is very important, a step that many beginners
forget. The results are invariably incorrect if this step is skipped--and
possibly even "random," since the status of the carry flag can be on or
off when the subtraction operation is performed. This can make debugging
difficult.
Breakout Game (BASIC)
The "Breakout" game involves the simplest animation technique available
on the Atari, moving individual pixels from one position to a new
position. We have a Graphics 5 pixel-sized ball that bounces around the
screen. It will ricochet off a movable paddle, the walls, or any of the 2
pixel-high by 5 pixel-wide colored bricks. Movement is accomplished by
erasing the ball at its old position and redrawing it at its new position.
The ball is very predictable. It changes direction only upon collision,
and in all cases (except contact with the paddle) simply reverses
direction. The point of contact with the joystick-controlled paddle
determines the ball's direction. Balls striking the left end travel
upwards and to the left at a 45 degree angle, while balls striking the
inside left travel in the same direction but at a 60 degree angle. Balls
striking the paddle's right side travel at similar angles, but to the
right.
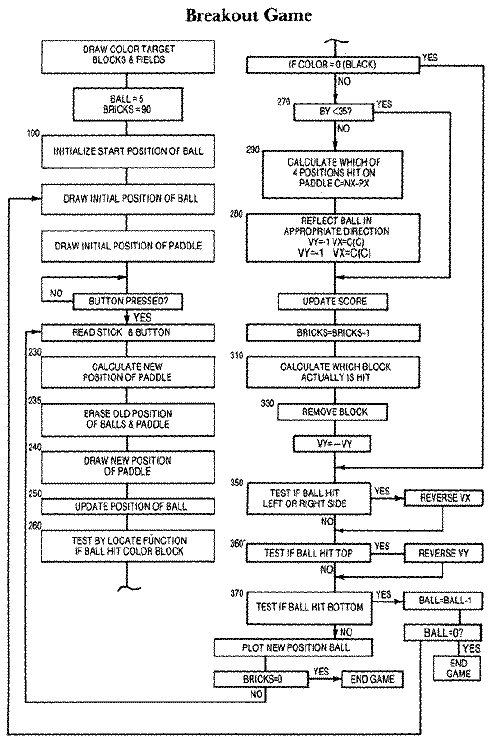
Once you have the design description, in this case a game that is an
old classic, the next step is to translate it into a logical sequence of
events and their consequences. This can best be accomplished by drawing a
flow chart that shows the possible pathways for each module in the
program. Each of these modules can be as small as a single statement, or
can consist of entire subroutines. No matter how detailed or general you
make it, the flowchart must accurately represent the game's logic. While
it is a good tool for learning to think logically, a flowchart isn't
necessary or required in all cases. Many good programmers have never drawn
one. They obviously have the ability to flowchart unconsciously in their
minds.
The game should be programmed in small steps rather than as a complete
entity. This way you get to see results early. Besides, it is easier to
debug a small section, such as the ball bouncing off the paddle and moving
around the screen, than to attempt to debug a complete program that is
full of errors. The most successful programmer will be one who can debug
by watching what goes wrong on the screen.
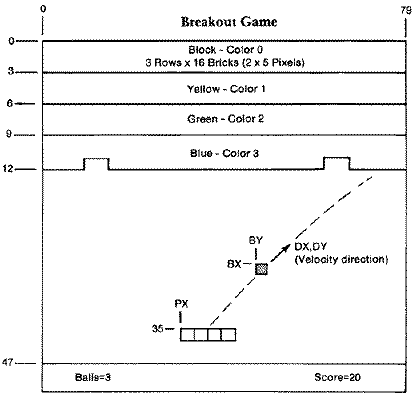
Paddle Position
Determining where the ball strikes the paddle is easy in our "Breakout"
game. The paddle is always drawn two-pixels wide at row 36 decimal or $24,
and the first pixel begins at PX, a variable controlled indirectly by the
joystick. Actually the new paddle position is P = P + D where D depends on
the direction of movement and whether the button is being pressed. If the
joystick is pushed to the left, D=-1, while if it is pushed to the right,
D=1. When the button is pushed, D=D*3, and the paddle moves at triple
speed. The Boolean logic in line 230, ((P+D)>0 AND P+D<76) gives a
value of true=1 or false=0 depending on whether the paddle has exceeded
the screen bounds after movement. If it hasn't, the result is P=P+D*(1),
and there is a new paddle position. If it has, the result is P=P+D(0) and
the paddle remains stationary.
Ball's Position & Velocity
It is easy to compare the ball's new vertical position NX to that of
the paddle's leftmost position PX. The difference NX-CX is C. You can use
this value to index into a table to obtain the new horizontal velocity; DX
= C(C). These values vary with position. The two outside blocks give a DX
of + 1 or 1, and the two inside blocks give a DX of +1/2 or -1/2. The
vertical velocity, DY is equal to -1 since the ball is always travelling
upwards after striking the paddle.
In order to update the ball's position, we take the old ball's position
and add the change in position or its directional velocity. The format is:
NEW POSITION = OLD POSITION + CHANGE IN POSITION
NX = BX + DX
NY = BY + DY
Incrementing or decrementing the ball's position by 1/2 in the X
direction is not physically possible since screen positions are whole
numbers. The ball's position is truncated to the nearest integer value
with the INT function. The result is that the ball remains stationary in
the X direction during one frame, then moves one whole pixel position
during the next frame or cycle.
Collisions with Bricks
As the ball bounces around the screen it will soon collide with one of
the colored 2 by 5 pixel-sized bricks at the top of the screen. It is
possible to test for a collision by using the LOCATE function. This
function, which returns the color register at the ball's position, works
only in BASIC Graphics modes 3-8. Non-zero values in this example indicate
a collision with one of the three colored bricks (Playfields #1-3).
If there is a collision, the correct block needs to be removed. This is
quite simple to calculate for the X direction:
C INT(NX/5)*5
You still need to determine if the ball hit the brick in an even or odd
pixel row. It might appear that the ball would always collide with the
bottom or odd row of pixels first, but if there are gaps between bricks as
occurs later in the game, the ball can approach from the side and strike
the brick along the top or even row of pixels. If the ball strikes the
bottom row, you will need to adjust the position to the brick's top row in
order to erase one complete brick. The test is a very simple Boolean
function in line 320. For example if the ball's new vertical position,
NY=9, then NY/2 <> INT(NY/2) would reduce to 9/2 <> 4 which is
true. We would then decrement NY to an even number in order to erase the
complete block. The top left corner of the 2 pixel by 5 pixel brick is
C,NY. Five pixels are erased from C,NY to C+4,NY in each of its two rows.
The brick's score depends on its playfield color. SCORE = SCORE +
SCORE(C), where C is the value returned by the locate function. The yellow
(playfield #1) bricks at the top are worth ten points, the green
(playfield #2) bricks in the middle are worth five points, and the blue
(playfield #3) bricks at the bottom are worth only three points.
The ball's vertical direction of travel reverses upon collision with a
brick. It continues in the horizontal direction until it reaches either
the left or right playfield boundary at BX=0 or BX=79. It reverses
direction there so that DX = -DX. If the ball reaches the top of the
playfield at BY = 0, it will reverse its vertical direction. But if the
ball reaches the bottom it is lost and we begin again with a new ball. The
game will end when we have run out of either bricks or balls.
Download
BREAKOUT.BAS (Saved BASIC)
Download
/ View
BREAKOUT.LST (Listed BASIC)
Breakout Game (Assembly Language)
The "Breakout" game is quite easy to translate into Assembly language
once you understand how BASIC handles its graphics commands. The Operating
System (OS) implements each of these commands through the CIO (Central
Input/Output) subroutine located at $E456. When a program calls the OS
through this location, the OS expects to be given the address of a
properly formatted IOCB (Input Output Control Block). There are eight of
these, each sixteen bytes long. These are located from $340 to $3BF. The
appropriate IOCB number times 16 is passed to the subroutine in the
X-register. The full details of how the internals actually work are really
not important, especially to the beginning Assembly language programmer.
Let's just say that we developed a set of graphics subroutines that mirror
their BASIC language counterpart. We have commented on each of these in
the listing for anyone who would like to study them.
Graphics Commands
The five graphics commands that we need for our game are: GRAPHICS #,
POSITION H,V; PLOT H,V; DRAWTO H,V; and LOCATE H,V,Color. We set up each
by inputting certain parameters into the Accumulator, X-register, and
Yregister. Once you've set up the registers you need only JSR to that
subroutine. The table below shows what you need to input into each of the
registers. Function Accumulator X-register Y-register
GRAPHICS Mode # ------- -------
POSITION Vertical Horizontal Horizontal
High byte Low byte
PLOT Vertical Horizontal Horizontal
High byte Low byte
DRAWTO Vertical Horizontal Horizontal
High byte Low byte
LOCATE Vertical Horizontal Horizontal
High byte Low byte
Has color
value on
return.
For example, if we wish to set up a Graphics 5 screen and draw a blue
(playfield #3 default color) line from 10, 15 to 30,15 our program would
be as follows: LDA #$05 ;GRAPHICS 5 SCREEN
JSR GRAPHICS
LDA #$03 ;PLAYFIELD #3
STA COLOR
LDA #$0F ;VERTICAL=15
LDX #$00 ;HORIZONTAL HIGH BYTE
LDY #$0A ;HORIZONTAL LOW BYTE
JSR PLOT ;PLOT PIXEL
LDA #$0F ;VERTICAL=15
LDX 000 ;HORIZONTAL HIGH BYTE
LDY #$IE ;HORIZONTAL LOW BYTE
JSR DRAWTO ;DRAW LINE
Breakout Game
Once you understand the simplicity of duplicating the BASIC graphics
statements in Assembly language you can proceed with developing the game.
The "Breakout" game is a very close translation of the BASIC version
with a few subtle differences. One of the problems in working with
Assembly language is that all numbers are whole integer numbers. In the
BASIC version the ball's horizontal direction (DX) became +1/2 or -1/2
when it hit the inner portion of the paddle. Since incrementing the ball's
position by +1/2 would be impossible in Assembly language, DX and BALLX, a
temporary value for the ball's horizontal position, are doubled in value.
If we then divide BALLX by two before plotting the ball's true position,
TX, the fractional part, will vanish. In essence the ball will move
horizontally every other frame.
BALLX = BALLX + DX (doubled values)
TX = BALLX / 2
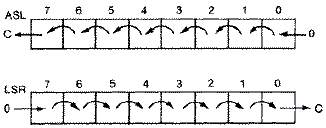
ASL and LSR Instructions
Multiplication and division by powers of two is easy in Machine
language. The mnemonic ASL is used for multiplication by two. The
Arithmetic Shift Left (ASL) instruction shifts all of the bits in the
Accumulator one position to the left. Thus, bit 0 is shifted into bit 1,
bit 1 into bit 2, etc. Bit 7 is shifted into the carry bit so that you can
use the BCC and BCS instructions to test for overflows. For example, if
only bit 2 was on (4 decimal) and we did an ASL, the bit would be shifted
to bit 3 (8 decimal). Thus, it is easy to multiply by powers of two by
performing repeated ASL instructions.
Conversely, division is performed by the Logical Shift Right (LSR)
instruction. Bits are shifted to the right and the bit 0 is shifted into
the carry. This is equivalent to dividing by two with loss of the
fractional part.
LDA #$05 ;LOAD ACCUMULATOR WITH 5
LSR ;DIVIDE BY 2
STA $4000 ;VALUE STORED IN $4000 IS 2
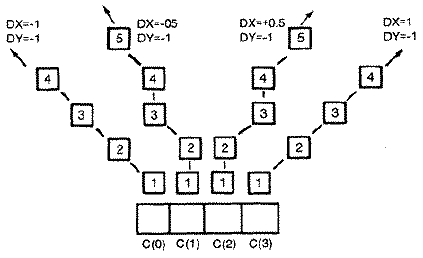
Ball's Direction After Paddle Collision
The table of directional values for the four possible collision
positions with the paddle are stored in VX. The two negative values in the
table are stored in their two's complement form because it is easier to
add two positive numbers rather than to test for a negative number and
subtract. 0th 1st 2nd 3rd
VX $FE $FF $01 $02
For example, #$FE (-2)+ #$03 = #$01. The offset position from the
paddle's left edge is placed in the X register to get the new horizontal
velocity. LDA TX ;COMPARE PADDLE HORIZ. WITH BALL HORIZ.
SBC PX ;DIFFERENCE
TAX
LDA VX,X ;FETCH VELOCITY VALUE FROM TABLE
STA DX ;THIS IS DOUBLED VALUE
We calculate the ball's new position as follows; CLC
LDA BALLX ;OLD BALL POSITION (DOUBLED)
ADC DX ;NEW HORIZ. VELOCITY DOUBLED
STA BALLX
LSR ;DIVIDE BY 2
STA TX ;BALL'S TRUE HORIZ. POSITION
Scorekeeping
The scorekeeping routine also deserves an explanation. It differs
substantially from the routines used in the other Machine language games
in this book. It takes advantage of the 6502's ability to work in a
numbering system called Binary Coded Decimal, or BCD. This system uses the
lower four bits or low-order nibble to represent the low-order decimal
digit, and the high-order nibble to represent the high-order decimal
digit. The advantage is that the numbering system resembles decimal. The
disadvantage is that it requires some advanced programming technique to
isolate the digits in order to print them to the screen. DECIMAL BINARY HEX
(BCD)
07 0000 0111 $07
10 0001 0000 $10
16 0001 0110 $16
42 0100 0010 $42
To get to this mode you must set the decimal flag with a SED (Set
Decimal Mode) command. It remains in effect until it is cleared by a CLD
(Clear Decimal Mode) command.
A pair of bytes, SCORE and SCORE+ 1 are used to store the four score
digits. These are updated by adding POINTS,X to SCORE+ 1 each time a brick
is removed. The X-register contains the color value of the block hit so
that we need only index into a table of point values. We didn't clear the
carry when we added #$00 to SCORE (highbyte). However, if there was an
overflow in SCORE+1 (low byte) during the first addition, the carry would
be included in the resulting value in SCORE. Each of the four nibbles must
be separated, translated into an internal character #, and finally placed
into the appropriate position in the text window. The byte's high nibble
is first shifted to the low nibble by four successive LSR instructions and
then translated into an internal character number. Digits in the internal
character set begin at #$10. Internal character #16 decimal = 0, 17
decimal = 1, etc. The ORA #$10 instruction, which combines the individual
bits in its operand with those in the Accumulator, is just a fancy way of
adding $10 to the value of our digit. The value of the low nibble is
isolated by ANDing it with #$0F. It is then ORed with #$10 to obtain the
internal character and stored in the next screen position. We have
effectively stored the thousands and hundreds digits in the screen window.
The code loops back again to obtain the value for the two nibbles in
SCORE+ 1. These contain the tens and units digits. All of the store
operations are done using indirect indexed addressing of the form
STA(WINDOW),Y. We will discuss this at greater length in later chapters.
Meanwhile, it allows us to index rapidly into a memory area whose two-byte
address is stored in zero page.
If you're confused or lost at this point, don't worry. Just read on.
Our intention was merely to show how a simple game like "Breakout" could
be translated into Assembly language using graphics subroutines. It is not
necessary to understand all of the details but to be able to roughly
follow the code as it pertains to the game's flow chart. Many of the
subtle tricks we mentioned in the previous discussion we will discuss in
much greater detail in subsequent chapters.
Download
BREAKOT.EXE (Executable program)
Download
BREAKOT.OBJ (Object code)
Download
/ View
BREAKOT.LST (Assembler listing)
Download
/ View
BREAKOT.S (Source file)
Download
/ View
BREAKOT.RAW (As printed in book)
Return to Table of
Contents | Previous
Chapter | Next Chapter
|
|



