|
Chapter 5
Player-Missile Graphics
Player-missile graphics differ from playfield graphics in two distinct
ways. First, the players, which appear as semi- transparent overlays
against the background, are memory independent of the playfield graphics.
Thus, these sprites, as playermissiles are sometimes called, don't
overwrite playfield memory and don't destroy the background graphics as
they move around the screen. Second, since they are directly mapped to the
screen by the CTIA/GTIA and the ANTIC hardware chips, positioning a sprite
on the screen is extremely fast and accurate. They were designed with fast
smooth motion in mind.
As we learned from character graphics, the screen is a two-dimensional
image; the screen RAM is organized one-dimensionally as one long string of
bytes. Animating a character requires erasing the old character image,
calculating a new position, then writing a new character image at the new
position. Unfortunately, if the motion is vertical, the new position must
be some multiple of twenty or forty bytes apart from the original in
memory. The necessary calculations are time consuming. Moreover, character
graphics animation with 8 x 8 pixel sized characters isn't smooth unless
you use numerous transitional shapes. Also the background needs to be
restored after each move.
Atari engineers thought of a simpler and better method to achieve
smooth animation. They created a graphics image that was both
one-dimensional on the screen and one-dimensional in memory. This image
appears as a vertical stripe one byte or eight pixels wide extending from
the very top of the screen to the very bottom. The image or player appears
in RAM as a table of bytes that is either 128 or 256 bytes long. Each
byte, depending on the programmer's choice of resolution, is mapped into
either one or two horizontal scan lines.
The two hardware chips, the CTIA/GTIA and ANTIC, automatically place a
sprite on the screen. While the GTIA is busy putting color pixels on the
screen based on graphics information furnished by ANTIC, it simultaneously
keeps track of its current horizontal position on the screen. If it finds
that the current horizontal position equals the value of the horizontal
position register for the player, it asks ANTIC to give it a byte from the
player-missile area of memory corresponding to the current scan line. It
then interprets that byte as a series of on-off pixels or points, starting
with the high bit on the left, and plots them in the selected player
color. If the bit in the byte is on, it illuminates or plots a pixel, and
if it is off it skips plotting the pixel. Areas of the player stripe that
contains zeros or no player data are transparent to the background or
playfield graphics. Scan lines that contain data form a solid image that
overlays but does not affect the background image.
Player data is mapped in much the same way as character data is mapped
in a character set. Where a character is limited to eight rows of data, a
player stripe, depending on player resolution, consists of either 128 or
256 rows. Each byte corresponds to a row, and each of its eight-bit
positions corresponds to the eight pixels that collectively form part of
the player image. A bit that is on or has a one in it lights the
corresponding pixel which maps from left to right, high bit to low bit.
For example
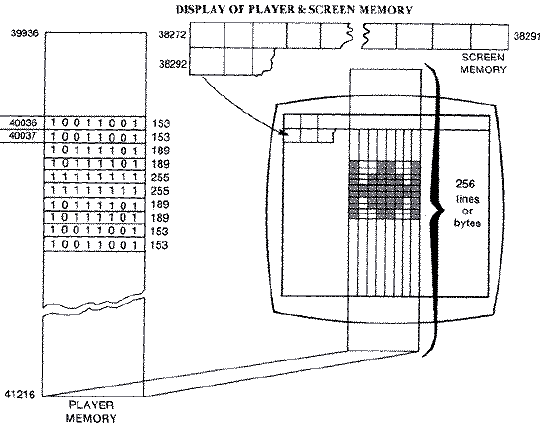
This data table, which is stored in the player-missile area of memory,
is 256 bytes long. Actually, only 192 bytes corresponding to the screen's
192 scan lines are effectively used. A 256-byte area was chosen since it
is one page of computer memory, and it is easier to find the start of a
player's data when it begins on a page boundary.
The vertical starting position depends on the position in player
memory. However, the 0th or first byte is mapped automatically by hardware
to an area offscreen past where ANTIC is generating display list scan
lines. Therefore, the first twenty or so bytes and the last thirty or so
bytes are beyond the normal raster scan of a television set. A player that
begins in the thirty-fourth position in player-missile memory will map to
the screen starting at the second scan line. Players move vertically by
moving the player data through the 256-byte page of player memory. The
higher a player image is stored in memory, the lower it appears on the
screen.
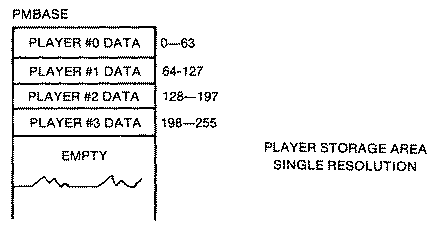
Atari's player-missile system consists of four players and four
missiles that reside in a 2K block of memory known as the player-missile
memory area. Think of
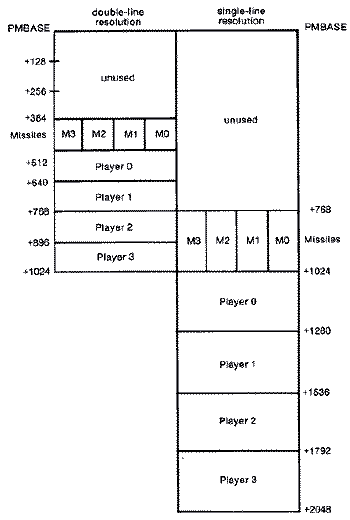
missiles as narrow players two pixels wide instead of eight pixels
wide. Each of the four players has its own playermissile area of memory.
Single-resolution players use 256 bytes or one page of memory, while
double-resolution players use 128 bytes or half a page of memory. They are
arranged sequentially so that player one follows player zero, etc. The
four missiles, on the other hand, are stored in the same block of memory
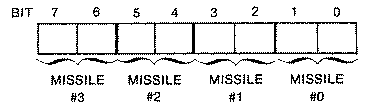
just below player zero. They are arranged in two-bit pairs with the 0th
missile occupying the rightmost or lowest twobits, and the third missile
the leftmost or highest two bits. While this arrangement is handy if you
want to combine all four missiles to enable a fifth player, it presents a
problem when moving a single missile vertically on the screen. If the
missile data is moved in memory to correspond with a missile's screen
movement, then portions of data for the other missiles that reside in
those same bytes will also be moved. There is a Machine language solution
to the problem that requires masking the bytes during movement, but this
technique is unavailable from BASIC except by a complex USR function.
Fortunately, horizontal movement is much easier. The designers
incorporated a separate horizontal position register for each player and
each missile. Even if all missiles are combined to enable a fifth player,
each two-bit-wide missile band must be still set individually.
Essentially, the fifth player is kept as a unit when it is moved, if each
missile is positioned two units apart in the horizontal axis when it is
moved.
The color and size of each player and its associated missile can also
be specified. Size only affects the horizontal width of the player or
missile. Widths can be normal, double, or quadruple size. For example, in
double width, the GTIA chip begins double plotting the bytes on bits when
it reaches the horizontal position register of the player or missile.
Color is assigned to four shadowed player-missile color registers. Since
these four additional color registers are independent of the playfield
color registers, more colors can appear on the screen at any one time.
While each player can have a different color, each missile is assigned the
color of its corresponding player. Thus, if player three is green, missile
three will also be green. The only exception to the rule is that if a
fifth player is enabled, the four combined missiles use the color in
playfield three's color register. There is rarely a conflict since
playfield three is only used in four graphics modes. Since the GTIA plots
both the player and playfield color pixels simultaneously, it can detect
any overlap between graphics images on the screen.
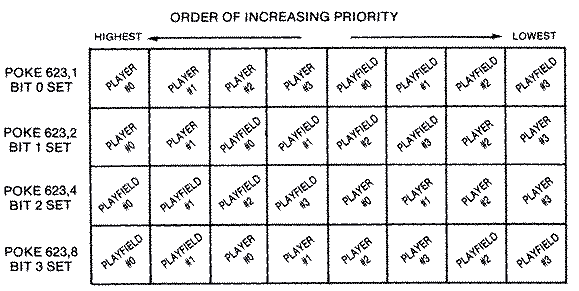
Player priority can be set so that all or half of the players are in
front of the playfield graphics, all are behind the playfield graphics, or
some of the playfield colors are in front of the players with the rest
behind. Any overlaps in position are of course returned in a series of
read-only hardware locations called collision registers.
These are quite useful in game design. You can also enable bit 5 in the
priority register (POKE 623,32) so that you obtain a third color when
players 0 and 1 or 2 and 3 overlap. If you don't set the overlap option,
the area of overlap will be black.
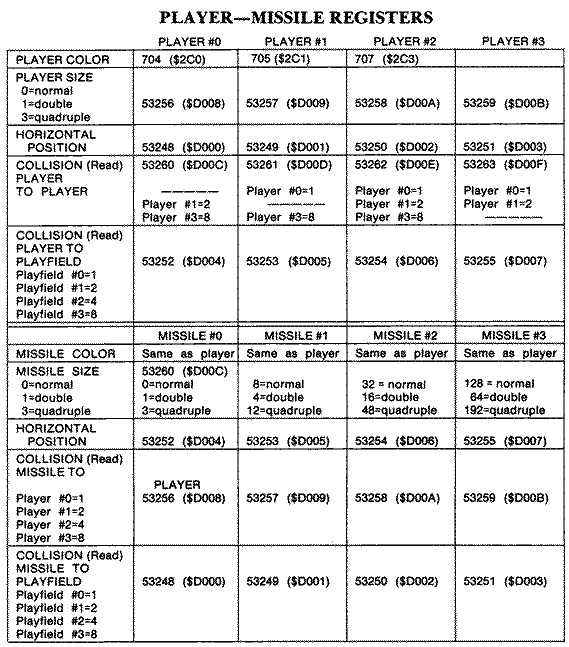
NOTE: Above values will set all missiles the same size.
NOTE: If missile sizes are set Individually, then add the four
different values. The combination is poked into ($D00C).
Enabling Player-Missile GraphicsThere are numerous steps involved
to enable player-missile graphics from both BASIC and Machine language.
Beginners see it as a long list of mysterious POKEs, but there is a
logical and explainable reason for each. First there are two electrical
switches between Antic, GTIA, memory and the world, which tell them
whether to do DMA (Direct Memory Access) automatically. The first, called
DMACTL (Direct Memory Access Control), is shadowed at location 559 decimal
($22F). It enables ANTIC to fetch bytes automatically and plot them to the
screen. When it is turned off with a zero, the screen is turned off
because ANTIC can no longer fetch bytes from memory. It defaults normally
to standard playfield graphics with double-line resolution for
player-missiles turned off. This value is 34 decimal. The table below,
which depends on which bit positions are set in DMACTL, summarizes the
various modes.
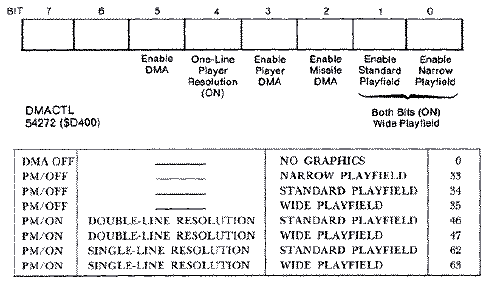
The second switch GRACTL (Graphics Control) physically enables
playermissile graphics. If we POKE a three into decimal location 54279
($D01D), both players and missiles are turned on. In addition, we will
need to set color, width, and horizontal positions for each player.
Next we need to reserve space for our 2K player-missile area in memory
assuming we are using single-resolution P/M graphics. Since it needs to be
on a 2K memory boundary, it is best to reserve space and put it above the
screen and display list areas beginning at eight pages (2K) below the top
of memory. This is accomplished by simply adjusting the top of memory
pointer at location 106 decimal with a new value that is eight less than
the original value. The computer now thinks top of memory is 2K lower than
it actually is, and assigns screen memory and its accompanying display
list below that when any graphics mode is set up.
The 2K player-missile area (single-line resolution) begins at the new
top of memory which we just POKEd into location 106. Since ANTIC needs to
know where we have put our P/M storage area, we need to POKE this value
into location 54279 ($13407) known as PMBASE. This is the high byte value
of the location. The low byte value is assumed to be zero since it is on a
2K page boundary.
The memory area assigned to player-missile graphics may or may not
contain miscellaneous data which will appear as garbage in the P/M
stripes. The 2K area should be cleared to zeros. However, since a long
series of POKEs in BASIC is rather slow, it is faster to clear only the
P/M memory that you will actually use. In the example below, only player
#0 is used. Therefore, only the area from PMBASE+ 1024 to PMBASE+ 1280 is
set to zero. In the worst case where you were using the missiles and all
the players, the unused first 768 bytes in singleline resolution or the
first 384 bytes in double-line resolution need not be cleared.
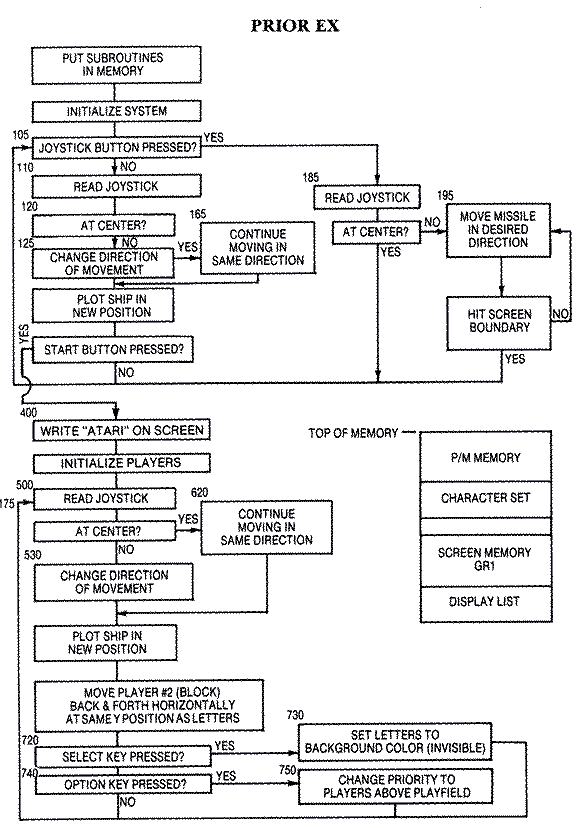
Space Ship ExamplePlayer #0 is a spaceship originally five scan
lines high. To make it appear larger each scan line is plotted twice and
the width is doubled. In addition, a pair of zeros has been placed at both
the top and bottom of the player image for a total of fourteen bytes. The
reason for this will shortly be clear. The fourteen player-missile data
bytes are then POKEd into the proper P/M memory area for player #0. By
POKEing the data starting at SPOT = PMBASE+1024+100 the player will begin
100 scan lines from the top. Since the first thirty-two scan lines are
above the top line of text on the screen, our image begins sixty-eight
lines from the top. Accounting for the two blank or zero lines of our
image, our ship actually begins at the seventieth scan line.
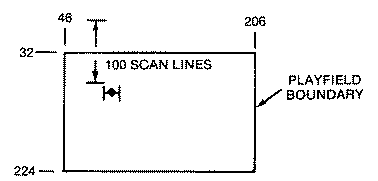
For a player to move vertically, all of its data needs to be shifted in
memory. Players can move downward on the screen by shifting the data
upward in memory. Conversely a player moves upward on the screen by moving
its data downward in memory. The laver case is definitely the easier
direction because data can be moved from top to bottom without the danger
of overwriting any of the bytes during the move. All fourteen bytes of
data are shifted upward two scan lines from SPOT+I to SPOT+I-2. The two
extra zero bytes on the end serve to erase the bottom two bytes of the
ship's shape in its previous position. If this isn't done, the bottom
sliver of the ship will remain as screen garbage after the move.
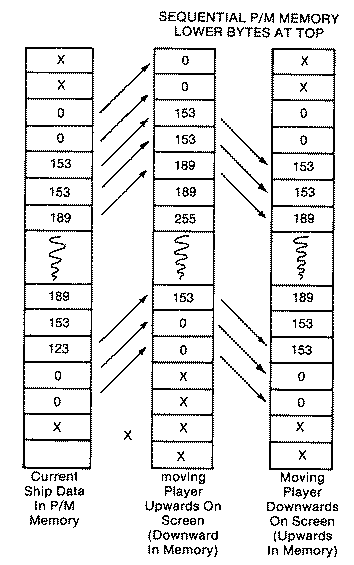
Moving the ship down the screen or upward in memory is slightly harder.
If we start at the top of the shape as before, the first byte (0) would
replace the third byte (153), and the second byte (0) would replace the
fourth byte (153). Fine, but when we try to move the third byte to the
fifth position, the original data (153) has been overwritten by the first
move. Eventually all of the bytes will contain zeros and the shape will
disappear. The solution to this dilemma is to start at the bottom of the
shape and move each of the bytes upward in memory two places. Since you
don't overwrite any shape information during the move, the shape remains
intact. Again, the two extra zeros at the top serve to erase the tiny
two-line sliver that would have remained after the move. It might seem
strange that we deliberately added two zero bytes at the top and two at
the bottom of our player when the rest of the storage area is obviously
full of zeros. However, these could only be used if more bytes than that
of our actual shape were moved, and only if we adjusted where the top or
bottom of our shape begins. If we need to go to this trouble, it is easier
to add extra leading and trailing zeros.
Download
PMEXAMP1.BAS (Saved BASIC)
Download
/ View
PMEXAMP1.LST (Listed BASIC)
A Player-Missile Machine Language Move SubroutineIt becomes
apparent from this simple example that moving a player vertically using
POKEs in BASIC is very slow. However, moving a player horizontally is fast
because a horizontal position register was built into the hardware.
One clever approach to moving players fast vertically is to take
advantage of BASIC's fast string-handling capabilities. These routines are
just high speed Assembly language copy routines. The trick to using these
routines is to fool the Atari into assigning the player-missile string
data to the memory area assigned to player-missile graphics. Then
player-missile graphics data can be moved simply with P$ = S$ type
statements. While this technique allows the programmer to avoid Machine
language subroutines, it is not the easiest method to learn or understand.
Since the example and explanation would be intimidating to beginners, we
will delay it until much later in this chapter.
Player-missile graphics can be speeded up tremendously if Machine
language subroutines are used. There have been numerous vertical blank
player-missile subroutines published in the magazines. While most are
effective in rapidly moving players vertically by one of several
techniques, nearly all have neglected missile movement. This is
unfortunate since moving one missile without disturbing the others
requires using AND and ORA machine instructions on a bit level to mask off
the other missiles during vertical movement. This is something that is
beyond the capabilities of BASIC.
We have developed an easy-to-use Machine language subroutine that can
handle both players and missiles simultaneously. The subroutine resides in
page six of memory but is relocatable to virtually any free area of
memory.
There has been much controversy on whether page six of memory is
actually a safe area for placing user subroutines for BASIC programs.
While it is true that inputting more than 128 characters into the text
buffer will overwrite the beginning of page six, any program-especially a
game that remains in control throughout-has no problem. In any case, the
second half of page six $680-$6FF is always safe.
Our subroutine was designed for single-line resolution player-missile
graphics. It requires the input of five variables: player number, player
length, the old Y (vertical) position, the new Y position, and the new X
(horizontal) position. The format is:
A = USR (1536, PLAYER #, PLAYER LENGTH, OLD Y, NEW Y, NEW X)
The number 1536 ($600) is the starting location of our subroutine. The
players are numbered 0-3 and the missiles 4-7. Player #4 in our subroutine
is actually missile #0, etc. The player length can only be as large as
sixtyfour lines. This limitation will become clear when we explain how the
subroutine works. The values for both the X and Y positions can be
anything from 0-255. However, you should be aware that only X values in
the range of 48-207 and Y values in the range 32-223 are within the bounds
of the 40 by 24 text screen or playfield graphics area. The range is
actually slightly larger, but visibility depends on the overscan of your
television set. While the OLDY value is the programmer's choice upon
initialization, it must be set equal to the NEWY position after each USR
call. If OLDY isn't set to NEWY immediately after the subroutine call,
unpredictable graphics will begin to appear in the player stripe when the
subroutine is used again. The reason is that the subroutine zeros out the
shape at its previous position OLDY before drawing the shape again at its
new position NEWY. If OLDY isn't set to the player's last vertical
position, the subroutine will miss zeroing the shape at the old position.
Most likely, you will get two shapes or, worse yet, a sliver left at the
previous position.
A Player-Missile ExampleThe next example is a simple
demonstration of the speed, versatility and ease of use of our
player-missile subroutine. This two-part example is instructive in several
regards. First, it shows how a simple spaceship capable of firing missiles
can be joystick controlled. Even its simple inline code, which allows
either the ship to move or the missile to move, but not both
simultaneously, gives some insight into the difficulty in designing even
the simplest games. Second, the concept of priority, or which player or
playfield is to be drawn in front of another is demonstrated. But first I
think a discussion of how objects move might be helpful, especially to
beginners.
Dynamics of Objects in MotionAny object in motion, whether it is
simulated on a video screen or moves in the real world, is subject to the
laws of physics. Readers will immediately cringe at the thought of
advanced mathematics, mainly calculus. But calculus is merely a method of
calculation that involves the summation of many small bits and pieces of a
body's velocity and acceleration to determine the actual distance an
object travels. Fortunately, the computer automatically divides our time
frame into analogously small units, or animation frames.
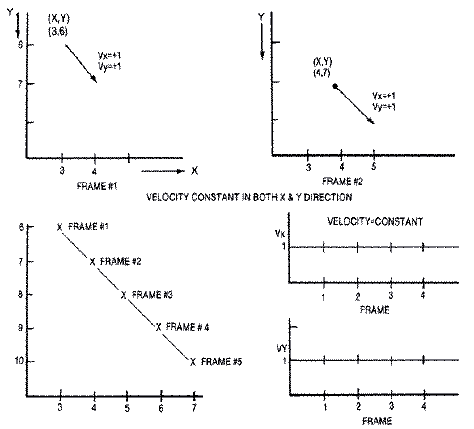
Let's examine an object in simple linear motion. The object is
initially at rest. It is then given a horizontal velocity of one unit to
the right. Thus the velocity is +1 unit/time frame. During each animation
frame, the object moves +1 units to the right.
An object's direction of travel and its magnitude is represented by a
line segment called a vector. An object's velocity always points in the
direction of travel. Our object shown below has a velocity of +1
units/time frame, so that the velocity is pointing to the right. Since the
velocity vector is to the right, the object moves to the right +1
unit/frame.
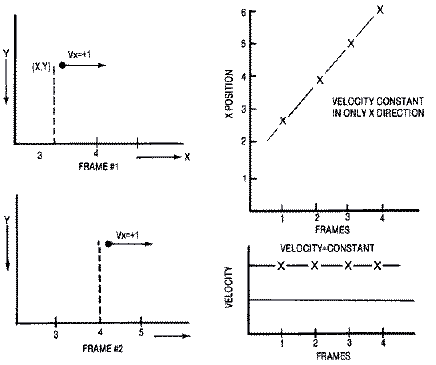
Similarly, an object that moves diagonally downward and to the right
has a positive velocity vector in both the X and Y directions. This
velocity vector is a combination of the velocity components in both the X
and Y directions. The object will continue moving in the direction of the
velocity vector until either VX or VY changes. For example, if VX becomes
zero, the object will begin to move straight down in the direction of the
new velocity vector.
This can be formalized into equations for each of the two screen
directions X and Y.
VX = +1 Velocity is constant in X direction.
X = X + VX New
position is the old position plus the change in position (velocity).
Likewise:
VY = +1 Velocity is constant in Y direction.
Y = Y + VY New
position is the old position plus the change in position (velocity).
While this simplistic method of moving objects by instantaneous changes
in direction and velocity works on the video screen, objects in the real
world don't behave this way. Take the family car for example. You step on
the gas pedal, and the car's velocity begins to climb steadily. The
distance traveled each second begins to increase as the velocity
increases. When the car is only going 15 MPH the car travels only 22 feet
each second, but when the car reaches 60 MPH it travels 88 feet each
second.
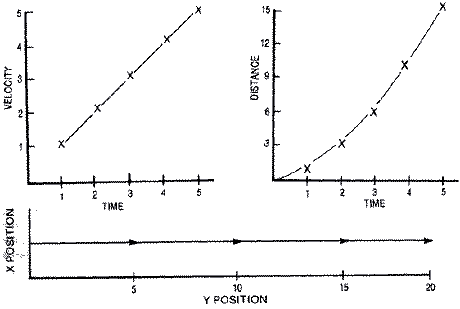
The driving force that speeds up our car is called acceleration ( V = V
+ A ). Acceleration can be constant as in a rocket's thrust, or like
gravity which pulls a falling object to Earth. For a screen object's
motion to appear realistic, especially in the case of a falling bomb,
acceleration must be taken into account. When a bomb drops, its vertical
velocity increases with time. If there were no wind resistance, the bomb's
vertical velocity would increase until its impact on the target.
If a constant force was suddenly applied to a stationary object such
that it accelerated downward with an increase in velocity of one unit/
frame, the distances moved would grow substantially.
TIME VELOCITY POSITION (distance)
0 0 0
1 1 1
2 2 3 VX = VX + 1
3 3 6 X = X + VX
4 4 10
5 5 15
6 6 21
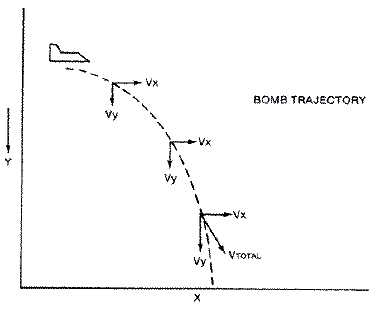
The plot of the trajectory of a falling bomb is shown below. The
trajectory, neglecting wind resistance, forms a curve that is called
"parabolic." There are two components to the velocity vector. VX in the X
direction is a constant set equal to the plane's forward velocity. VY in
the Y direction grows larger with time as gravity accelerates it in the
downward direction. This same effect can be observed by dropping a ball
from the second or third story of a building. At first, the ball falls
slowly, but then it begins falling faster. Observers at ground level will
note the acceleration of the moving ball just before it bounces. The
summation of the two velocity vectors determines the resultant direction
of an object's motion for each animation frame. Since the VY vector grows
larger with each frame, the total velocity vector begins to point
downward. Eventually, the bomb will be falling almost straight down. Thus:
VX=CONST X=X+VX
VY=VY + GRAVITY Y = Y + VY
In the above cases, the acceleration was non-existent or constant.
However, as we will see at the end of this chapter, even simple games
involving a steerable spaceship that can be thrust in the direction that
it is headed, must use variable acceleration. The rate or value may remain
constant but the direction changes. While only the beginning of the
discussion above is necessary to follow the second example, I hope it will
give you some insight into how an object's motion is simulated on the
Atari's video screen.
Program InitializationOur first example, a joystick-controlled
single ship capable of firing missiles in eight directions, takes
advantage of our player-missile Machine language subroutine. As in the
first example in this chapter, a 2K block of memory needs to be reserved
for player-missile graphics. The top of memory pointers are moved down
eight pages, and the player-missile base PMBASE is set equal to the top of
memory. BASIC then sets up the screen area and its display list just
below. Graphics I was chosen because it uses little screen memory and
because we will need to write some large characters to the screen for the
second part of our example.
Next, our two Machine language subroutines need to be POKEd or placed
into memory. The first subroutine is the player-missile subroutine. It is
151 bytes long. Since it begins at the start of page six ($600) or 1536
decimal, a simple FOR ... NEXT loop that reads the data statements and
POKEs memory, will do the job. The second Machine language subroutine is a
clear memory routine. It will automatically clear player-missile memory to
zero in a fraction of a second. It replaces a slow thirty second long FOR
... NEXT loop which would POKE a zero into each sequential memory location
from PMBASE+0 to PMBASE+2047. It also resides in page six of memory,
beginning at $6A0 or 1696 decimal. It is twenty-six bytes long.
We must activate player-missile graphics next. We will set DMACTL for
singleline resolution and GRACTL for both players and missiles. Player #0
is set to double width by writing a zero to location 53256, and player #2,
which will be used in the second part of this example, is set to double
width by writing a one to location 53258. The missiles are set to regular
width, and the color of each of the players is selected. The priority
GPRIOR shadowed at location 623 decimal is set so that player #0 is in
front of the playfield graphics and player #2 is behind. We will talk more
about this location during the discussion of the second half of this
example. Last, we tell ANTIC our player-missile address by writing it to
PMBASE at decimal location 54279. Since our subroutine also needs the
location of PMBASE, its high byte is. POKEd into location 1686 which is
the last memory location of our subroutine. We could have passed it to the
subroutine via the USR function, but then you would have had to type the
value in each time you used the subroutine.
Player Shapes Using the P/M SubroutineWe then store the two
player shapes in our player shape storage area. You will recognize the
first shape from the first example. It is our spaceship. The second shape
is a solid block ten bytes high. Normally, you would want to POKE your
shapes into the proper place in the player-missile memory area. However,
when we designed the subroutine, we felt that the best and fastest
approach would be to erase the shape at its old location before redrawing
it at the new location. The traditional approach was to do a memory move
of the entire shape including leading and trailing zero bytes, to insure
pieces aren't left behind. If a shape were moved vertically more than one
or two scan lines, a series of small memory moves had to be done
sequentially.
In order to use our faster subroutine, we had to find a safe place to
store our shapes in memory, no matter where you put our subroutine, the
player-missile area, and screen memory. Fortunately, the first 768 bytes
of the playermissile memory area are unused. We decided to use the first
page or 256 bytes for the player storage area. This limits the size of
each of the four players to sixty-four bytes. Since sixty-four bytes or
scan lines make up nearly one-third of the screen, this limitation really
doesn't cause any problems.
Before any shapes are stored in this "safe" area, player-missile memory
should be cleared or zeroed with the Machine language subroutine stored in
page six of memory at 1536 decimal. The only parameter passed via the USR
function is the starting memory address PMBASE. This routine was
specifically designed to clear eight pages of memory, precisely that of a
2K block of player-missile memory. If you neglect to clear it, random
patterns will most likely surround your shapes in the player missile
stripes. The first shape, our spaceship, which is player #0, is POKEd into
the first ten bytes of the player-missile storage area from PMBASE+0 to
PMBASE+9. The second shape, the solid block, which is player #2, is stored
beginning at PMBASE+128.
The spaceship (player #0) must have an initial starting position and
starting velocity. While it is obvious that the present position X0=100,
Y0=80 is important, its previous Y axis position must have an initial
value despite the fact that there couldn't have been a previous one.
Setting Y0OLD=80, the value of our present Y position, will suffice.
Likewise, the same is true for player #0's missile. YM0OLD=10, a value
that insures that it is off screen.
Joystick Controlled Ship MovementThe spaceship's velocity is
joystick-controlled. Pushing the stick in any direction instantaneously
changes the ship's velocity. If the stick is pushed to the right, the ship
is given a horizontal velocity of 2 units/frame. Since there is no
vertical component to the ship's velocity, the ship will move to the right
2 units/frame. It will continue in that direction until either it collides
with the screen's boundary, or a new joystick input gives the ship a new
velocity vector. The equations that control the ship's X and Y position
are as follows.
X0 = X0 + VX0
Y0 = Y0 + VY0
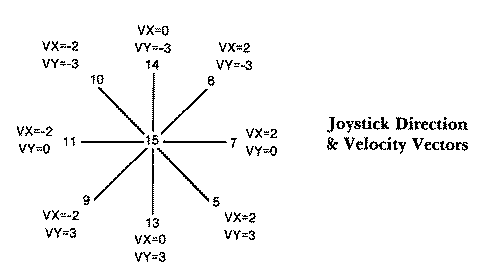
There is a separate pair of velocity vectors for each of the eight
possible joystick directions. The absolute values on each of the axis are
not the same because pixel size is rectangular rather than square. Objects
with equal velocities along both axis tend to move faster along the
horizontal axis than along the vertical axis. To compensate for this, we
set VX = 2 and VY = 3. Diagonal velocities, which are the vector sum of
the two velocity components, are faster than anticipated. While it appears
that you could correct this by using fractional values for both velocity
vectors on the diagonals, you can't move part of a pixel position in
either axis. However, if the velocity vectors were much larger you could
correct the diagonal velocity by using smaller whole numbers. The diagram
below shows the velocity component values for each of the joystick
directions.
The only way to set the ship's two velocity vectors for each joystick
direction is to test the value of Z0 = STICK(0) against each of its
possible values. When the stick is centered (Z0=15) the velocity remains
the same and we skip the remainder of the tests. The other eight
possiblities are tested in a series of IF statements. If a match is found
for any direction, new velocity vectors are substituted. While it appears
to be a cumbersome method, there is no better method.
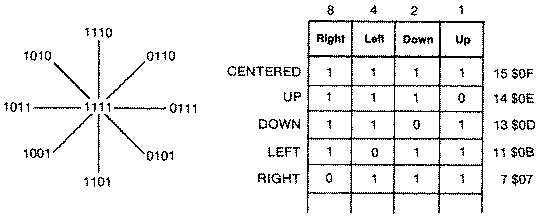
I'm sure many readers wonder why Atari BASIC returns such a strange and
illogical set of values for joystick directions. STICK(0) through STICK(3)
reflect values returned in the PIA chips locations 54016 and 54017
($D300,$D301). When the joysticks are centered, each of the four bit
locations for each joystick are on (set to one). When the joystick is
pushed in any direction, its appropriate bit position is turned off (set
to zero). For example, if the joystick is pushed to the right, the fourth
bit from the right is turned off. The remaining three on bits add up to
seven. Diagonal joystick movements have some combination of two bits
turned off. The diagram below shows all of the possible bit patterns.
After the joystick is read, the player's position is updated and
checked so that it does not exceed the screen boundaries in either
direction. A USR call to our playermissile Machine language subroutine
will move the player shape into the proper place in memory so that it
appears at the choosen X,Y screen coordinates. The format as discussed
earlier is A = USR (1536, PLAYER #, PLAYER LENGTH, OLD Y, NEW Y, NEWX).
The player length is 10, OLDY equals Y0OLD in this example, NEWY equals
Y0, and NEWX equals X0. Immediately after the USR call, update the OLDY
position with the NEWY position so that you don't have to worry about
losing this value when you calculate your new position during the next
frame.
Missile MovementPressing the joystick button fires a missile.
STRIG (0) is normally set to a one value when the button isn't pressed.
But when the button is pressed it becomes zero and the program branches to
a second joystick read routine at line 185. It is nearly identical to the
first, with the exception that the velocity vectors are nearly double in
value; VXM0=5 and VYM0=6. This ratio produces nearly identical apparent
speeds in both the horizontal and vertical axis. Since the missile needs
to be given a direction to fire, it branches past the missile routine if
the joystick is centered.
The missile's initial starting position is at the center of our ship.
Since X0, Y0 are the coordinates of the ship's missile at the center of
the ship, the missile's initial position equals the current ship's
position plus the correction. Thus, XM0=X0+3 and YM0=Y0+4. The missile's
position is updated each frame the same way the
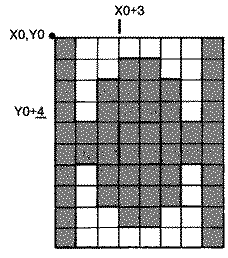
ship's position is updated each frame. The new position equals the old
position plus the missile's velocity vector.
XM0 = XM0 + VXM0
YM0 = YM0 + VYM0
Unlike the ship, however, the missile's velocity vector can't be
changed once the missile is fired. Missile movement is in a closed loop
that exits only when the missile reaches the boundaries of the screen.
This closed loop not only prevents you from firing a second missile before
the first has reached the end of its travel, it also prevents the ship
from moving while the missile is in motion. This is a good example of how
simplistic code that branches to either one event or the other creates an
unrealistic effect. The solution, which will be explained in the next
example, requires the ship's movement code to be placed in line with the
missile's movement code, and conversely the missile's movement code to be
placed in line with the player's movement code. This apparent overkill, in
fact, allows the ship to be steered once the missile is launched.
The missile is plotted via the USR call to our player-missile
subroutine. Missile #0, which is two pixels wide, is player #4 and its
height is set to two scan lines to make it square shaped. Its OLDY
position is YM0OLD, and its new position NEWX, NEWY is XM0, YM0. Again,
once the subroutine is called via the USR call, it is important to
immediately set the missile's old position equal to its present position.
Finally, if the missile does reach the screen boundaries, it is
necessary to place it out of view beyond the scan of the television set.
Since the missiles can't be simply shut off, you should set the horizontal
register to either a small number or a large number. Since XM0=10 is
offscreen, it will suffice.
Priority DemonstrationThe second part of the example is a
demonstration of player versus playfield priority. Whenever two
independent objects such as two players or a player and a playfield object
appear at the same spot on the screen, the GTIA must decide who gets
displayed first and who second. This is known as priority. There is a
register called GPRIOR shadowed at location 623 decimal ($26F) that
selects which screen object is in front of the others. There are actually
only four possible selections. Either all of the players are in front of
the playfield, all of the playflelds are in front of the players, players
#0 and #1 are in front of the playfields with players #2 and #3 behind, or
playfields #0 and #1 are in front of all the players with playfields #2
and #3 behind.
Lower number players take precedence over higher number players and,
likewise, lower number playfields take precedence over higher number
playfields. Actually, there is no way for two playfields to occupy the
same space, since each color pixel is assigned to a specific color
register. In fact, only the on bits, or those portions that show in the
player-missile stripe, actually are involved in the priority conflict. The
off bits are ignored by the system. Obviously, if a player has the shape
of a donut, the background or another higher numbered player set behind it
will show through the hole.
Unfortunately, player #0 always has priority over the other three
players. There is no method to change the priority between the individual
players other than to switch the player data between player-associated
areas of memory.
The great advantage of priority control is that you can control what
happens to players when they meet the background color display. Perhaps
you have an aerial combat game. You may want the plane to fly behind
clouds, yet always remain in front of the scrolling ground far below.
Setting bit three in GPRIOR will give two of the playfields higher
priority than the players, and the remaining two playfields the lowest
priority.
In our example, we have the word ATARI written in playfield #0, a
spaceship (player #0), and a moving block (player #2). Initially, bit I is
set in GPRIOR (POKE 623,2) so that player #0 moves in front of the letters
while player #2 moves behind the letters. This part of the example can be
reached by pressing the START key. The IF statement in line 175 tests for
this possibility. The spaceship is joystick-controlled exactly like the
first part; however, the missiles have been disabled.
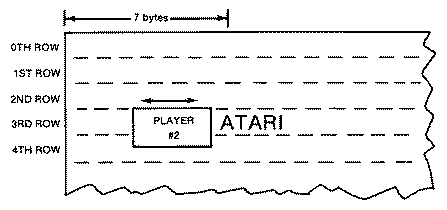
Pressing the SELECT key sets the color of the letters to the same color
as the background. However, since the pixels in the letters still refer to
playfield #0, and player #2 had a lower priority than all of the
playfields, that player is masked by the invisible playfield object as it
moves behind it. Our much larger player shows through the spaces around
the individual letters, thus illuminating the darkened object.
Pressing the OPTION key does two different things. First, it restores
the playfield #O's color to its default color and luminance. Second, it
changes the GPRIOR to I so that all players have priority over all
playfields. Now both our block and our spaceship are in front of the
letters. The ship (player #0) still has priority over the moving block
(player #2).
Download
PMEXAMP2.BAS (Saved BASIC)
Download
/ View
PMEXAMP2.LST (Listed BASIC)
Explanation of Player-Missile SubroutineThe player-missile
subroutine was designed to handle both players and missiles
simultaneously. In order to do this while retaining compact and
relocatable code, several compromises were made. First, only single-line
player resolution is offered. We felt that the coarser, double-line
resolution could be simulated by setting the player-missile stripe at
double width, then double plotting each of the shape's bytes. An attempt
to give you a choice of resolution modes would have created a long and
messy algorithm since the memory requirements of each are quite different
mathematically. In single-line resolution the actual memory storage areas
for each player are exactly one page or 256 bytes apart. This makes
setting the pointers to the memory area easy since only the high byte is
involved. But in double-line resolution the memory areas are 128 bytes
apart. A much more complicated multi-byte add is required to set the
pointers.
Second, we decided to erase the old shape completely before drawing the
player shape in its new position. It is a faster technique since the more
traditional method needs to do a series of block memory moves to shift the
shape more than one line at a time. Our method requires storing the shapes
in a permanent safe spot. We choose the first 256 bytes of the
player-missile area. Since there are four player shapes, each shape is
limited to 64 bytes or scan lines.
Advanced Assembly language programmers will notice that we did not
write the subroutine in VBLANK. We felt that BASIC was slow enough without
adding small delays while waiting for the VBLANK interrupt to begin our
subroutine. Moving several players and their corresponding missiles on the
screen at the same time could slow the game down. Motion smoothness is
another reason for using VBLANK for player-missile graphics. However, as
you will see in the following game examples, the animation frame rate is
not fast enough to produce smooth animation with or without VBLANK.
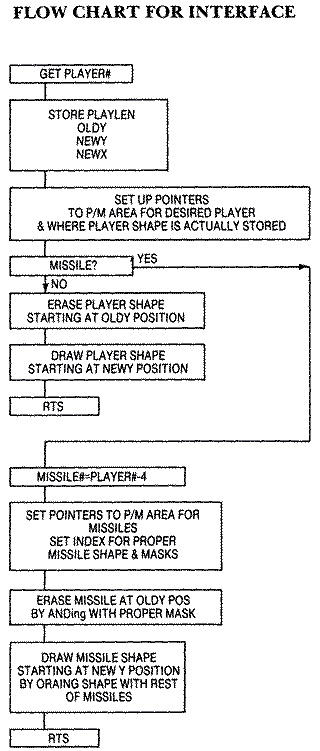
The subroutine is divided into three parts: a routine to interpret and
store the passed parameters in the USR function; a routine for erasing and
drawing the player shape; and a routine for erasing and drawing a missile.
Once the parameters are stored, a test on the player number determines if
it is actually a missile, and if so, branches to that part of the code.
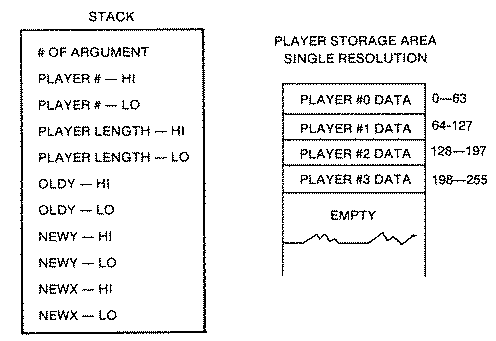
Interpreting USR Parameters
A USR function in BASIC pushes all of its parameters onto the stack
before it enters the Machine language subroutine. The stack is like a dish
dispenser in that the last value placed on the stack must be pulled off
first. The first byte contains the number of passed parameters, a useless
value, and one to be discarded. The other parameters are stored in
two-byte pairs, high-byte first, in the order that you passed them, The
high-bytes in our example are useless since none of our values exceeds
255. The five pairs are pulled off the stack in an indexed loop using the
X register. They are pulled two bytes at a time. Only the second, or low
byte is stored sequentially at PLAYNUM,X ($691, X). Thus location $691
contains the player number, $692 the player length, $693 the value for
OLDY, etc.
Erasing and Storing Player ShapesThe pointers to move our player
or missile shape from their storage area to the proper player-missile
memory area are set up next, The shape is stored at SHAPEL, SHAPEH. The
high byte BASE is just the beginning of the P/M storage area which was
POKEd into location 1686 decimal ($696) from BASIC. The low byte is
obtained from a table called INDEX. Each of the values in this four-byte
table are sixty-four bytes ($40) apart. The actual memory location that
the shape is to be stored at in the P/M area is SHPML, SHPMH. Since each
player is 256 bytes or a page apart in memory, we added #$04 to BASE in
order to set it for player #0. We then did a cute little trick. We put it
in a loop and incremented SHPMH for each player number.
Erasing the old player shape from memory could be handled quite easily
with simple indexing in the form STA ADDRESS,Y if only one single player
were involved. ADDRESS would be the absolute address of that player's P/M
memory, and the Y register would contain the value YOLD. Unfortunately,
the high byte of each player's P/M memory area is different. Rather than
try to update ADDRESS each-time, it is more efficient if the two-byte page
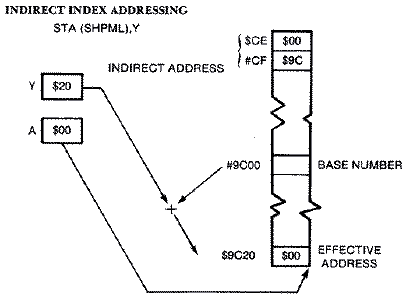
address is stored in zero page. Then indirect index addressing in the form
STA (SHPML),Y can be used either to erase or plot player-missile data.
If the computer finds a $00 in location $CE (SHPML), and a $9C in
location $CF (SHPMH), then the base address is $9C00. The Y register
contains the value of the OLDY position. If the shape was thirty-two scan
lines down the screen, then the Y register = $20. If the computer wished
to erase the shape, then it would store a #300 in the Accumulator into
memory location $9C00 + $20, or $9C20 as shown:
The actual code to erase the player shape is reiterated in a loop
PLAYLEN times. Since it is easier to increment the Y register from zero
until it is equal to PLAYLEN, the vertical screen offset is stored in
SHPML in zero page. The address SHPML, SHPMH is now the address of the
beginning of the player-missile shape. The Y register offsets into the
shape. The code is shown below. ERASE LDA OLDY ;Y VALUE
STA SHPML
LDA #$00 ;ERASE WITH 0
TAY ;Y REGISTER = 0
.1 STA(SHPML),Y ;STORE IN PROPER P/M AREA
CPY PLAYLEN ;DONE?
BLT .1
The code for drawing our shape is quite similar, except that instead of
storing zeros in P/M memory, we transfer the player shape from its storage
area to its proper place in P/M memory. The pointers to its storage area,
SHAPEL, SHAPEH were previously set up in zero page. We need update only
SHPML, the low byte pointer to the place we are actually moving our
player, with the NEWY position. The high byte SHPMH remains the same. The
code follows: LDA NEWY ;NEW Y VALUE
STA SHPML ;SETUP POINTER TO PLOT
LDY #$00
DRAW LDA (SHAPEL),Y;LOAD BYTE FROM PLAYER SHAPE TABLE
STA (SHPML),Y ;STORE IN PROPER P/M PLAYER AREA
INY ;NEXT BYTE
CPY PLAYLEN ;DONE?
BLT DRAW
Handling MissilesPlayer numbers 4-7 refer to missiles 0-3
respectively in our player-missile subroutine. If we didn't use different
numbers, the user would have to type in a letter M or P to differentiate
between the two different kinds of sprites.
While missiles are just narrow players, all four reside in the same
256-byte block or page of memory. The missiles, each of which is two bits
wide, are arranged parallel to each other. Essentially, all four two-bit
pairs for each scan line are in the same byte of data. This makes moving
one missile but not others somewhat difficult.
Missile #0 uses the first two or lowest two bits of the byte, missile
#1 bits three and four, missile #2 the fifth and sixth, and missile #3 the
two highest bits. While the data in one byte determines which pixels are
lit for all four missiles on any scan line, each missile has an
independent horizontal position register. Thus, each of the missiles can
have movement completely independent of the others.
As we mentioned, moving one missile vertically without changing the
other missiles' data. can be a problem. If we had just two missiles
initially on the same scan line, and we attempted to move missile #0
downward one scan line, either a memory move or an erase before redrawing
would affect the missile #1 as well. In the first case, missile #1 would
move in tandem with missile #0, while in the second case missile #1 would
be erased. The solution is to mask off the other missile's bits during the
erase, and to draw the missile's new position using another masking
operation that will not affect the remaining bits.
ORA InstructionThis drawing technique uses the OR memory with
Accumulator (ORA) instruction. It works on the bit level. If the bits in
either memory or the Accumulator are on, then the result is one. If
neither is on, the result is zero. ACCUMULATOR MEMORY RESULT BIT IN
BIT BIT ACCUMULATOR
0 0 0
ORA 1 0 1
1 0 1
1 1 1
If missile #0 was already on a particular scan line and you wanted
missile #1 to be on the same scan line you would ORA missile #1 with the
byte in P/M memory. 0 0 0 0 0 0 1 1 MEMORY
ORA 0 0 0 0 1 1 0 0 MISSILE SHAPE
0 0 0 0 1 1 1 1 RESULT
AND InstructionAnother selective drawing technique is the And
Memory with Accumulator (AND) instruction. It too works on a bit level and
is used to filter or mask out certain bits in the Accumulator. Both the
memory bit and the Accumulator bits must be set (on) for the result to be
one. If either memory bit is off, or both bits are off, the result is
zero. We put ones where we don't want to change bit values, and zeroes
where we do. We can erase one missile at a time without affecting the
others. ACCUMULATOR MEMORY RESULT BIT IN
BIT BIT ACCUMULATOR
0 0 0
AND 0 1 0
1 0 0
1 1 1
If you wish to erase only one of the two missiles on the same scan
line, you AND the data byte with a mask that always produces a zero bit
result in the missile bits to be erased, and a one in all the other bits.
For example, to erase missile #0 and not missile #2, the mask with which
you AND the data bit is $FC. 0 0 1 1 0 0 1 1 MEMORY
AND 1 1 1 1 1 1 0 0 MISSILE SHAPE
0 0 1 1 0 0 0 0 RESULT
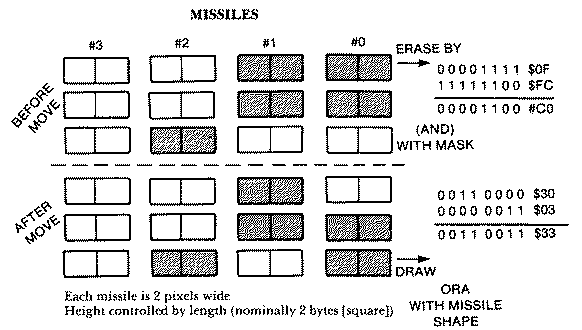
There are four different missile masks:
Missile mask #0 1 1 1 1 1 1 0 0 $FC
Missile mask #1 1 1 1 1 0 0 1 1
$F3
Missile mask #2 1 1 0 0 1 1 1 1 $CF
Missile mask #3 0 0 1 1 1
1 1 1 $3F
Likewise, there are four different missile shapes. For simplicity and
visibility we made each missile two pixels wide. The height is controlled
by the length, which is nominally two bytes, However, missiles can assume
tall, thin dimensions if the user chooses a length of four or more bytes.
Missile shape #0 0 0 0 0 0 0 1 1 $03
Missile shape #1 0 0 0 0 1 1 0
0 $0C
Missile shape #2 0 0 1 1 0 0 0 0 $30
Missile shape #3 1 1 0
0 0 0 0 0 $C0
The data for the above two tables appears in our player-missile
subroutine as MASKS and SHOTS.
The heart of the missile routine is the erase and draw code. Each is a
mere three lines long. The selected missile is erased by ANDing memory
with the proper mask. LDA (SHPML),Y ;LOAD OLD MISSILE DATA
AND MASKS,X ;ERASE IT BUT DON'T DISTURB OTHER MISSILES
STA (SHPML),Y ;STORE RESULT BACK IN MEMORY
The selected missile redrawn in its new position with the following
three lines of code. LDA (SHPML),Y ;LOAD OLD MISSILE DATA
ORA SHOTS,X ;MERGE SHOT DATA WITH OTHER MISSILES
STA (SHPML),Y ;STORE NEW COMBINED MISSILE BYTE IN MEMORY
The technique is best illustrated with an example where we have three
missiles on the screen. Missiles #0 and #1 are on the same two scan lines.
Missile #2 is on the same scan line where we wish to move our missile.
Download
PMINTB.EXE (Executable program)
Download
PMINTB.OBJ (Object code)
Download
/ View
PMINTB.LST (Assembler listing)
Download
/ View
PMINTB.S (Source file)
Download
/ View
PMINTB.RAW (As printed in book)
Two Ship ExampleWe can write a simple two-player shoot-'em-up
game in BASIC if we use our player-missile subroutine to provide enough
animation frame or speed for playability. The code for the second ship is
nearly identical to that for the first ship. In fact, with the exception
of using variables having a I at the tail end of the variable names, the
code is the same, line for line. The code for player #2 follows the code
for player #1.
The code for each player includes: a joystick read routine to determine
the ship's new velocity vector and to update its position; a similar
routine to determine the missile's velocity and direction; and logic to
prevent either the ship or the missile from leaving the screen boundaries.
The ship in our previous example stopped dead while the missile moved.
These ships, however, not only continue in their present course during the
missile flight; they even alter course to evade enemy missiles.
In the previous example, if the missile movement code was executed, it
branched past the player movement code. In this example, the missile code
updates the player position, and the player position code updates the
missile position. This enables the player to continue moving or
maneuvering while the missile is in flight.
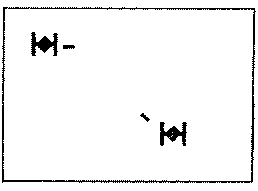
If you look at the game's flow chart for each player, you will notice
that the two possible paths are decided by whether the joystick button is
pressed. Pressing the button fires a missile in the desired direction,
only if there isn't another missile already on the screen. Of course, if
you don't give it a direction (joystick centered), it skips firing the
missile and just updates the ship's position based on its current heading.
When it fires the missile, it turns the missile flag on (M0FLAG = 1). To
prevent it from firing again before the missile reaches the edge of the
playfield, the program tests M0FLAG in line 430. If the flag is on, it
just updates the missile's position based on its current trajectory.
Finally, once the missile reaches the screen edge, it turns the flag off
(M0FLAG = 0) and plots the missile offscreen.
When the joystick button isn't pressed, the program code reaches line
110, the beginning of the joystick read routine which determines the
ship's new velocity vector. This enables the ship to change direction.
Thus, if a player wishes to change direction immediately upon firing his
missile, he must release the button quickly, so that it reaches this code
on the next animation frame.
Once a missile has been launched, it will continue on its path even
while the ship is being maneuvered. Therefore, the missile's position
needs to be updated in this pathway, too. This is done immediately after
the ship's position has been updated, but only if the missile is on the
screen.
Collision and ExplosionsA game wouldn't be complete if we
couldn't detect if one or the other ship were killed in combat. There are
two ways to die in this type of game-by collision with the opponent's ship
or by missile fire. The collision register at decimal 53260 ($D00C)
detects player #0 to player collisions. If it returns a value greater than
zero, two players have collided. Likewise, collision registers at 53256
($D008) and 53257 ($D009) detect collisions between missiles and players.
The first will return the value 2 if missile #0 collides with player #1,
and the latter will return the value I if missile #1 collides with player
#0. It is important that these collision registers are cleared to zero
before plotting players and missiles on the screen. You do this via the
HITCLR register at decimal 53278 (DO1E) in line 90. This line at the
beginning of the animation frame loop clears all of the collision
registers before any players or missiles are placed on the screen.
The rather simplistic explosions are linked to the sound routine. Each
ship brightens from luminance 4 to luminance 14 in its own color, then
blacks out quickly. The luminance changes within a low, rumbling sound
loop. The formulas in lines 1570 and 1580 were designed to prevent INT
(10-I*0.66) from becoming larger than the value 10. If the ship's
luminance of 4 when added to this value became larger than 15, the ship's
color and luminance would change as the color value would wrap to the next
higher color with a low luminance.
Recall that the sound statement is SOUND (Voice, Pitch, Distortion,
Volume). The pitch is set to 250, a very low tone, with a distortion value
of 4. The even numbered distortion levels 0,2,4,8,12 introduce different
amounts of noise into the pure tones, 10 and 14. The FOR ... NEXT loop
(lines 1150-1580) decreases the volume level very slowly.
This example's slow animation frame rate produces a game lacking
smoothness. BASIC is slow even with the use of Machine language
subroutines. There are a lot of IF ... THEN statements that slow the game
down. The game, however, will run a little faster if all of the REM
statements are deleted. Arcade games really need to be written entirely in
Assembly language to achieve fast, smooth animation. The Space War game
that is developed at the end of the chapter is a very similar game, but
smoother and more controllable.
Download
TWOSHIP.BAS (Saved BASIC)
Download
/ View
TWOSHIP.LST (Listed BASIC)
Shoot Bricks GameThe next example uses both playfield and
player-missile graphics in a timed game in which the object is to survive
the longest between two crushing brick walls. The joystick-manueverable
player can use a pistol to shoot any of the bricks out in the ten rows on
either side of him. The bricks are replenished randomly at a rate slightly
faster than the player can remove them. Thus, it becomes a matter of
strategy and endurance to last for any reasonable length of time.
When designing a game like this, you must anticipate the player's
strategy. The player, when confronted with the impossiblity of keeping the
entire wall back, will retreat to either the top or bottom and shoot just
at the blocks immediately surrounding him. If the bricks were still placed
on the screen randomly even after a row of bricks closed completely, the
player would have plenty of time to shoot at the few random blocks
appearing in the rows adjacent to him. However, if the random blocks are
not put on the screen in the already closed rows, bricks would appear more
rapidly in the few open rows. This makes the game fast-paced and somewhat
challenging. The game itself has little play depth, so don't expect it to
hold your interest as a game. It was primarily designed to teach
programming technique.
It is desirable to have a different color for each of the ten rows of
bricks, but there is a maximum of only four color registers in the
non-GTIA graphics modes. Therefore, we use display list interrupts to
change a single color register while ANTIC is drawing the screen. It would
be easier to use GTIA mode 11, but, unfortunately, this mode does not
support collision registers.
We choose to do the display in ANTIC 5, one of the non-BASIC graphics
modes, because the four-color characters are sixteen scan lines high. Each
of the lines contains forty characters. The blocks are four color dots
wide by 16 scan lines tall. The bricks are added and removed in adjacent
pairs (two characters) so that they appear to be square-shaped. The
availability of the extra colors had little to do with the initial
programming design, but when we put in a scorekeeping timer at the bottom
of the screen, we were able to draw the characters using a different color
register from that of the blocks. A collision is never detected when the
player touches the score line.
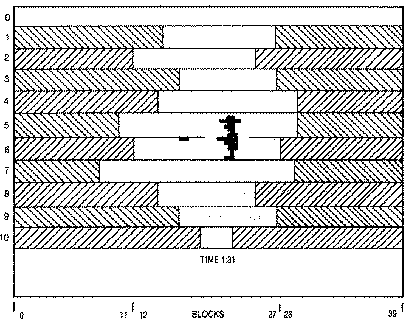
Setting Up Display ListThe screen resides just below the top of
memory which has been lowered twelve pages to make room for both the
player-missile memory and new character set. We choose to modify the
display list for a Graphics I screen because the display memory (20
columns x 24 rows) is the same as ANTIC 5 (40 columns x 12 rows), and our
display list is slightly shorter. The start of the display list, which is
shadowed at locations 560 and 561, is exactly the same for both graphics
modes. Therefore, it is easy to POKE in our new display list at DUST =
PEEK(560)+PEEK(561)*256. This value is 37216 for 48K machines. If we
substitute the following 20-byte display list for the original, we will
have an ANTIC 5 screen.
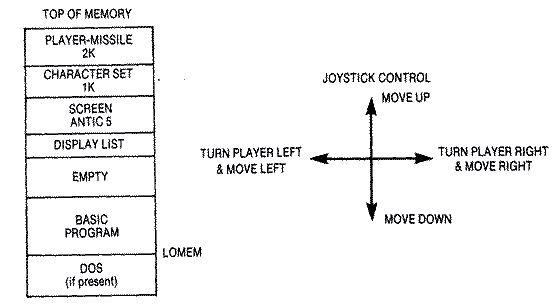
112 These three instructions print
112 24 blank scan lines at the top
112 of the screen
69 ANTIC 5 with a LMS instruction added
128 Address of the first line of screen data
145 145*256 +128 = 37248
133 Display the rest of the data in
133 ANTIC 5 with a DLI added
133 We have a total of 11 Antic 5 lines
133
133
133
133
133
133
133
7 Text mode 2 for timer display
65 jump and wait for vertical blank
96 Address of vertical display list itself
145 145*256+ 96 =37216
(return to the top of this list)
InitializationThe initialization for this game resembles our
previous example. The playermissile, clear memory, and display list
interrupt subroutines are each POKEd into memory in their appropriate
places in page 6. The code is stored as DATA statements. The first half of
the character set (512 bytes) is then moved to its new location, just
above the top of memory, starting at location CHRSET which is equal to
PEEK(106)*256. Only the first two characters are used to generate the
screen. The 0th character is a blank and is used where there are no
blocks. This includes our empty 0th row at the very top. The first
character is rewritten as a solid shape using color register 1. The bit
pattern for each line in the character is 10 10 10 10 decimal 170 or $AA.
Using this bit pattern for color register I is a deliberate choice. The
characters in the score line use color register 2. Thus, a collision with
our score letters and numbers (playfield 2) will not produce the same
value as a collision with a block (playfield 1).
Blocks are placed initially on the screen in rows I through 10 for
columns 0 to I I and 28 to 39. There are six pairs of blocks situated on
each side of the player on each row. The offset into screen memory for any
block is OFFSET = 40*R + C, where R and C are the row and column
respectively. The location of the screen is shadowed at locations decimal
88 and 89. With SCREEN = PEEK(88) + PEEK(89)*256, the actual memory
location of any block is SCREEN + OFFSET.
Player-missile graphics appear to be double-line resolution set at
double width, but they are actually single-line resolution with each byte
doubled. Two different players are used for the man. Player #0 faces left,
and player #I faces right. They are the same color and have the same
vertical position. Player #1 is placed on the screen initially at X=125,
Y=50.
The two levels of difficulty are selected with the SELECT key. It
toggles between putting blocks on the screen at one-half second intervals
and one second intervals. An asterisk (*) at the bottom right of the
screen denotes the easier level. The START key starts the game.
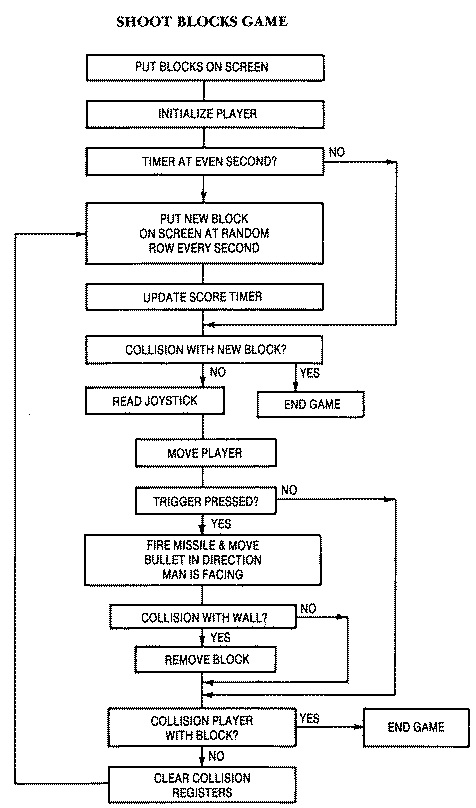
Main Game LoopThe game loop tests when to place a block randomly
on the screen at one-half or one second intervals. VBLANK increments the
timer at decimal 20 every sixtieth of a second. When it overflows (TIMER
>255), location 19 is incremented. If we set TIMER = 195, after sixty
cycles occur(one second), location 19 becomes 1. This makes a convenient
test to determine when one second has elapsed. Likewise if TIMER is set to
225 with the SELECT key, after one-half second location 19 would be
incremented. The'test at line 210, IF PEEK(19)=O THEN 344, skips putting a
new block on the screen and updating the scoring timer unless the proper
timing interval has elapsed.
There are two pointer arrays, L(10) and R(10), that keep track of the
inside wall boundaries closest to the player for each row. Initially each
of the L(I) elements are set to I I and each of the R(I) elements are set
to 28. As blocks are added and subtracted, these values begin to change by
multiples of two. For example, if a block were added to both the left and
right sides of row 3, then L(3)=13 and R(3)=26. If blocks were added just
to the left side, eventually the sides would touch when L(3)=25 and
R(3)=26. Since we don't want to add a block to a row that is already
touching, we could test if R(I)L(I)=I. If it equals 1, then we choose a
different random row and random side to try to place another block.
Eventually, we find a place even if it is in one of the rows to the right
or left of our player. The gun fighter can be maneuvered around the vacant
area of the playfield by a player using a joystick. When the joystick is
positioned up or down, the man moves vertically up or down by four units.
When the joystick is pushed left, a left-facing figure appears and moves
two units leftward. Similarly, a right facing figure appears and moves
rightward two units when the joystick is pushed right. The routine also
supports diagonal movements incorporating combinations of vertical and
horizontal movement. Each of the joystick movements sets the variable PLAY
to zero or one to indicate which player is to be placed on the screen
through our player-missile subroutine. The player that does not appear on
the screen is placed offscreen at X=10. Again remember to set the old Y
position equal to the new Y position (YOLD=Y) just after the subroutine is
used.
Collision TestA collision between either player and the playfield
#1 blocks has to be tested in two different places in the game code.
Obviously the test must be done just after the player moves, but it also
has to be done just after anew random block is placed on the screen. A
collision is detected in either case if the value 2 is set in player #0's
collision register 53252 ($D004) or player #1's collision register 53253
($D005). Since the bricks appear to be crushing our man, it is effective
to squash him by setting the player width back to normal. When this
happens, it appears that the man is compressed towards the left. This
occurs because the player image is always plotted from left to right and
begins at the value in the horizontal position register. The GTIA just
double plots player pixels when set to double width. The player struck by
the left wall remains in contact with the wall when it is compressed, but
the player struck by the right wall will shift to the left, or away from
the wall, eight pixels. If we just correct the X position by adding 8, it
will remain in contact with the right wall and look like it was also
crushed by the block.
While a collision between a missile and a block isn't difficult to
detect, the program must determine which block was hit. Obviously, the
block must be in the row directly in line with the pistol. If you look at
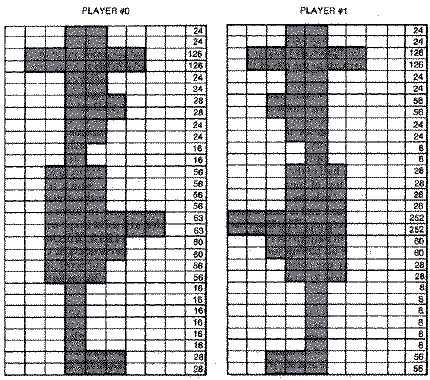
the diagram below, you will see that the pistol is sixteen scan lines
below the top of the man. Since the top left position of the man is at
X,Y, then YM = Y+ 16. The bullet fires from the tip of the gun at XM = X
when facing left, and at XM = X + 8 when facing right. The movement
routine prevents the pistol from going beyond the top of the first row of
blocks. When the pistol is at the top of the first row of blocks (YM = 48)
the man is at Y=32. Therefore, the formula ROW=INT((YM-32)/16) determines
which row the bullet travels. If we substitute YM = Y+ 16 the expression
simplifies to ROW=INT((Y-16)/16). For example, if the man is at the very
top (Y=32) then his pistol is aimed along ROW=INT(32-16)/16 or ROW=1 as
expected. The bullet moves 2 pixels horizontally each frame until it
eventually collides with a block. The pairs of blocks are then removed
from the side the player faces. Since the player can't move while the
bullet is in motion, there is no ambiguity possible. For example, if the
player (PLAY=O) were facing left on row 2, and the left block pointer
L(2)= 9, then blocks 2,9 and 2,8 are removed. You need only POKE a 0 into
locations SCREEN+OFFSET and SCREEN+OFFSET-1 where OFFSET 40*ROW + L(ROW).
Likewise, if a player were facing right (PLAY= 1), the two blocks that
need to be removed are at locations SCREEN+OFFSET and SCREEN+OFFSET + 1
where OFFSET = 40*ROW + R(ROW).
The game naturally ends when the player runs out of space. The stopped
timer indicates the time elapsed. At this point everything has to be reset
for the next game. The blocks on the screen are reset for the next game.
The blocks on the screen are reset slowly due to Atari BASIC's naturally
slow implementation of the POKE statement. This does give a breather
between games. The timer is reset, then the player. A button press is all
that you need to begin a new game.
Extra Colors via a Display List Interrupt Subroutine
Some of the advanced programmers might find the display list interrupt
subroutine to be of interest. It changes the color value in color register
1 ($2C5) each time ANTIC calls it via a display list -interrupt. Since it
keeps an internal counter called PLACE for its X register index, it must
know when to reset its pointer. It does this by checking the value in the
vertical line counter which increments by one for every two scan lines.
When it is equal to line 50, which is two scan lines beyond the beginning
of row # 1, it resets PLACE to 0. It loads PLACE into the X register,
indexes into the color table, and stores it in the color register. Now
PLACE is incremented by one. The next DLI just loads the next color in the
table into the color register. The pushes and pulls on the stack at the
beginning and end of our subroutine save the current X register and
Accumulator so that they are restored upon return to your program.
Download
SHOOT.BAS (Saved BASIC)
Download
/ View
SHOOT.LST (Listed BASIC)
Space War GameSpace War, the first game with a fully steerable
spaceship, was developed at MIT. While most of the newer computer owners
won't remember this game, practically everyone is familiar with Asteroids.
Most versions of this game have a fully steerable spaceship that can be
thrust in the direction that it is headed. Although some versions invoke
an automatic deceleration mode, some Asteroid games require the player to
turn his ship around so that it thrusts in the opposite direction to slow
down.
Dynamics of Motion with AccelerationWe demonstrated earlier in
this chapter that objects move in the direction of their velocity vector.
An object's new position is its old position plus its change in position
due to velocity.
Using the Atari's screen coordinate system for the example above, VY is
negative and VX is positive. Therefore,
X=X+VX
Y=Y+(-VY)
While the velocity vector may remain constant for many animation
cycles, so that a ship will continue to move in the same direction, sooner
or later a new velocity vector will be input to change the object's
course. This new velocity is the vector sum of the old velocity vector and
the new velocity vector.
Those readers who have taken Physics will recall that the velocity of a
body in motion changes due to external forces on it while it is in motion.
In spaceships, that force is thrust. Thrust causes an acceleration of the
object's mass as shown in the equation.
F=m*a=m* delta V
When thrust is applied to a spaceship, it accelerates. If a ship is
light and has a big engine with considerable thrust, it will accelerate
quickly. But if it is heavy, it will accelerate much slower. Acceleration
is essentially caused by a change in the object's velocity if you ignore
the object's mass,
Unless you are doing an actual simulation, in which the values of
thrust or force and an object's mass are important, only acceleration
values need to be considered. Suitable values for arcade games are small
and scaled, so that objects don't move fast relative to their size, or fly
off the screen in the blink of an eye.
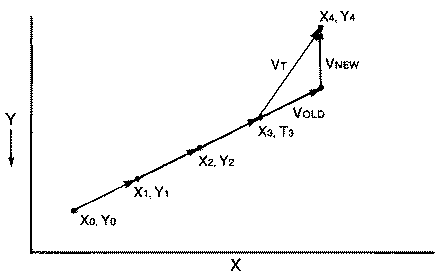
If we consider a spaceship that is in motion for three frames, then
thrust only during the fourth frame, it will change direction depending on
the vector sum of its old and new velocity vectors. This is illustrated
below. The applied thrust is straight upwards, so that VX = 0 and VY = -2.
The ship's new velocity vectors for each direction are calculated as
follows:
VX = VX(old) + delta VX = 2 + 0 = 2
VY = VY(old) + delta VY =
-1+(-2) = -3
Likewise, the ship's new position is equal to its old position plus its
change in position due to velocity for that animation frame. This breaks
dowq into components for the X and Y directions.
X = X(old) + VX
Y = Y(old) + VY
The ship's new velocity vector causes it to move two units in the X
direction and three in the negative Y direction during each frame until a
new thrust vector is applied. The resultant position can be summarized in
the table below. Frame X Y delta VX delta VY
0 10 100 2 -1
1 12 99 2 -1
2 14 98 2 -1
3 16 97 2 -3 Thrust applied here
4 18 94 2 -3
5 20 91 2 -3
Now, when the acceleration on an object, is sustained over many
animation frames, the increase in velocity is cumulative. For example, if
thrust were applied to a stationary object in the positive X direction
with a force of 1 unit/frame, the new VX would increase from zero by units
of one for each animation frame. CYCLE VX X CYCLE VY Y
0 0 0 0 0 0
1 1 1 1 2 2
VX=1 2 2 3 Similarly VY=2 2 4 6
3 3 7 3 6 12
4 4 10 4 8 20
Our example makes it clear that if you accelerate for too many
animation frames, the spaceship will be moving too fast. A limit should be
set on the velocity vector for both directions. just what the limit should
be depends on the effect you wish to achieve. Obviously, if your animation
rate is that of VBLANK, 60 frames per second, a ship velocity of 5
units/cycle will race across the screen in one-half second.
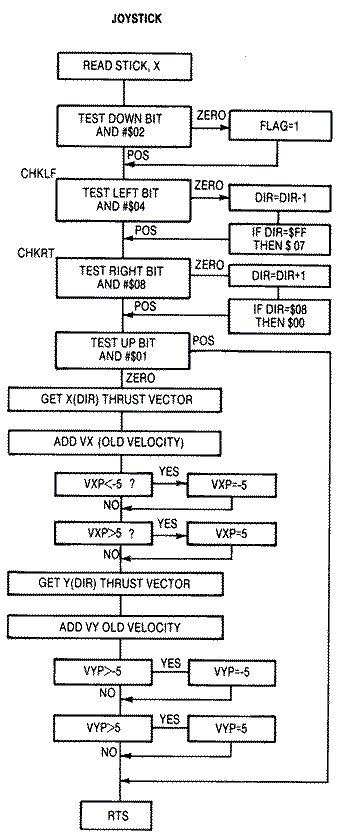
Joystick RoutineA joystick will control the ship's direction in
our game. Pushing to the left or right rotates the ship to one of eight
directions. Pushing up thrusts the ship. The joystick is read in the
VBLANK routine every 1/60th of a second. While a Machine language
subroutine is more than equal to the task of keeping up with the update,
its speed creates a small problem. If a player turns his ship by pushing
left or right on his joystick, the ship will spin rapidly, making 1/8 of a
turn every 1/60 of a second, That translates to 7 and 1/2 turns per
second, a speed that is obviously uncontrollable. The joystick must be
read less often, say every sixth VBLANK cycle if the ship is to turn
slowly enough to steer.
Machine language joystick routines are inherently simpler because only
four bit positions for up, down, left and right, need to be tested.
Diagonals are usually ignored because they nearly always represent
combinations of commands. For example, a diagonal up and right command in
our game means thrust while turning right. The joystick read subroutine
will detect the bit pattern twice, once when testing the up bit to
determine if it should reset the velocity, and a second time when testing
the right bit to determine if it should turn the ship. The bit pattern is
as follows. X X X X RIGHT LEFT DOWN UP
128 64 32 16 8 4 2 1
All of the bits are normally set when the joystick is centered or in
the neutral position (I I 1 1). When the joystick is pushed in any
direction its particular bit position is turned off, as illustrated in the
diagram below.
To test a particular bit position you only need to AND it with that
bit. For example, to test if the left bit is turned off:
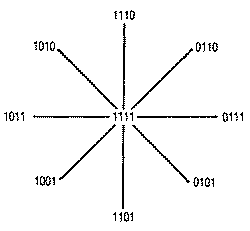
00001010 Diagonal left & up
00000100 AND #$04
00000000 Result=0
The result is zero if the bit is turned off when the joystick is
being pushed in that direction. If the joystick were in the neutral
position, the third bit would be on, and the result after the AND
operation would be non-zero. When the result is zero we want to decrement
DIR, the ship's direction, and make sure that if it becomes negative ($FF)
it is reset to #$07. The code is as follows. All of the code is indexed
with the player number in the X register. CHKLF LDA STICK,X ;READ JOYSTICK
AND #$04 ;LEFT BIT
BNE CHKLF ;BRANCH IF NOT ZERO
DEC DIR,X ;DECREMENT THE SHIP'S DIRECTION
LDA DIR,X ;CHECK IF NEGATIVE
CMP #$FF
BNE .1
LDA #$07 ;SET DIR=7
STA DIR,X
.1 JMP CHKFD ;CAN'T BE RIGHT IF PUSHED LEFT
CHKRT LDA STICK,X
Pushing forward on the joystick thrusts the spaceship. ANDing the
joystick value with #$01 tests the up bit. If the result is zero, the
joystick has been pushed up. The acceleration or thrust vector depends on
the ship's direction. If the ship points to the right, DIR = 2, then VXT =
1, and VYT = 0. If the ship points diagonally upward and to the left, DIR
= 7, then VXT = -1, and VYT = -1.
Ship's Direction and Velocity VectorsNote that many of our ship's
directions produce negative velocity values, while others produce positive
values. Separate routines are required for adding and subtracting in
Machine language. BASIC, however, just adds a negative number (X = 5+
(-1)). That's the clue. Adding a negative number is exactly the same as
adding a positive number in Machine language. The difference is that
negative numbers, like -1, are represented by the two's complement which
for -1 is $FF. There is a limit for signed numbers of + or -127, because
the BMI instruction tests the carry bit and considers the value if set.
With the simplification of our thrust vector addition problem, we can
construct a table of velocity vectors for each DIR value.
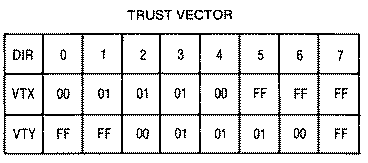
The equations for the ship's two velocity vector components are as
follows:
VXP = VX(old) + VTX(DIR)
VYP = VY(old) + VTY(DIR)
A speed brake can be incorporated into the algorithm to prevent the
velocity from exceeding a preset value. This would be analogous to wind
resistance on a fastmoving automobile. It prevents a vehicle's speed from
increasing infinitely. I choose a maximum velocity of 5 units per frame.
It is based on keeping the animation smooth and the speed in bounds. The
code for the X direction is as follows: LDA DIR,X ;GET PLAYER DIR
TAY
CLC
LDA VTX,Y ;GET X(DIR) THRUST VECTOR
ADC VX ;ADD OLD VELOCITY VECTOR
CMP #$FA ;IS IT -6?
BNE .5
LDA #$FB ;CLIP TO -5
.5 CMP #$06
BNE .6
LDA #$05 ;CLIP TO 5
.6 STA VX
STA VXP,X ;STORE NEW SHIP VELOCITY IN X DIRECTION
Addressing the Correct Shape TableNow that we can control our
ship in eight directions, we need shape tables for each of these
directions. That means eight separate shapes, each twelve bytes long. The
plot subroutine that places the shape in the player-missile memory area is
virtually the same as that used in our player-missile subroutine discussed
earlier in the chapter.
The zero page pointers to our shape and to its eventual storage
location in player-missile graphics memory are set up in a subroutine
called PLOTSET0 for player #0 and PLOTSET1 for player #1. Since our
drawing routine takes the direction into consideration in order to obtain
the correctly rotated shape from our shape table, we can find the correct
low byte of the shape by the following formula:
SHPL = SHPLO(DIR)
The shape number DIR, which is also our direction, is placed in the Y
register so that we can find the low byte pointer to our shape stored in a
table called SHPLO. Each of the values in that table are twelve bytes
apart starting at #300. The high byte is constant for all shapes. LDY DIR ;VALUE FOR DIRECTION OF ROTATED SHAPE
LDA SHPLO,Y ;AS INDEX TO PROPER LOW BYTE OF SHAPE
STA SHPL ;STORE LOW BYTE POINTER IN ZERO PAGE
LDA /SHAPEO ;HIGH BYTE
STA SHPH ;STORE HIGH BYTE IN ZERO PAGE
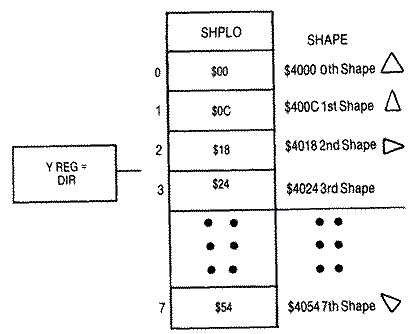
If the ship were turned so that it was pointing right, then DIR = 2 and
SHPLO(2) = $18. This low byte of the shape table is stored as SHPL. The
drawing routine will now plot the second shape from our shape table.
Smoothing the Ship's MovementRecall that when we updated our
ship's position in our last BASIC example, movement wasn't very smooth
because of the slow animation frame rate. Potentially, we face a very
similar problem here because the ship's velocity vector that controls its
next position is only updated every sixth frame. If the ship's position is
updated in the same loop as the ship's velocity, it will appear to have
very jerky movement, sometimes moving as much as five pixels per frame. It
would be better to move the ship in smaller increments more often, even as
fast as the scan rate of sixty times per second. Of course, at slower
velocities the ship would have to be moved less often. The trick is to
control the rate.
If the ship were moving in a direction at full speed, VX = 5, we would
want to update the position every frame, but if the ship were moving
slowly, VX = 1, we would want to update the screen every fifth or sixth
cycle. This means that we should skip plotting the ship at its new
position until a number of frames has passed. We could use a counter
called SKFLAG to check when we should plot. Naturally, it would be
different for each velocity and could be stored in a lookup table for easy
access. Its values would nearly be the reciprocal of the velocity. At VXP
= 5 we would want to replot each frame so SKFLAG = 1, and when VXP = 1 we
would want to replot every fifth or sixth cycle or SKFLAG = 6. The
relationship between the ship's movement and its actual velocity VXP isn't
exactly linear. If you look in the table you will notice that it is fairly
linear at slow speeds, but jumps from twenty pixels every sixty frames at
VXP = 3, to thirty pixels every sixty frames at VXP = 4, to a whopping
sixty pixels every sixty frames at VXP = 5. Fortunately, this is only a
game, and the discrepancy is not noticeable.
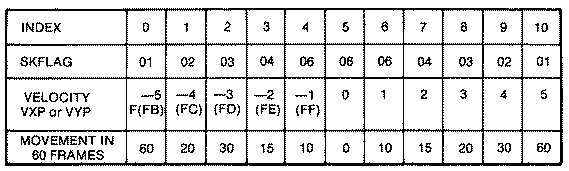
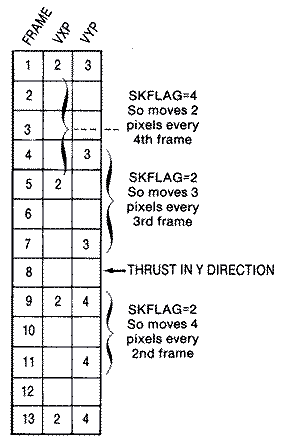
The code that determines when the ship is to be moved and replotted for
each direction is quite simple. The number of frames to skip, SKFLAG, is
obtained from our table based on the ship's current velocity and
direction. Five has been added to the velocity so that negative VXP, and
VYP values can be indexed, too, using the Y register. Counters for each
axis, SCRCNTX and SCRCNTY, that keep track of the number of frames elapsed
since the last screen update, are incremented. They are then compared
against the values from our table. When it matches, that counter is reset
to zero, and the player's position for that axis is updated and plotted.
The code for the X axis is listed below. UPDATEX CLC ;LOAD PLAYER'S HORIZ. VELOCITY
LDA VXP,X ;SO NEG #S APPEAR IN TABLE TOO
TAY ;USE AS INDEX
LDA SKFLAG,X ;GET VALUE FROM TABLE
INC SCRCNTX,X ;INC. COUNTER FROM LAST UPDATE
CMP SCRCNTX,X ;AT UPDATE TIME?
BGE .1
JMP EE ;NO! DON'T UPDATE
.1 LDA #$00 ;RESET COUNTER
STA SCRCNTX,X
LDA VXP,X ;BEGIN UPDATING PLAYER POSITION
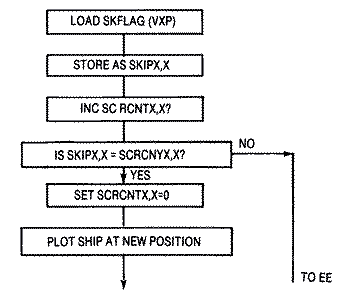
Each time the player's position is updated in either axis, the player
moves one pixel position in the proper direction. If the velocity is
negative, the player moves either to the left or up depending on which
axis is being updated. If the velocity is positive, the player moves down
or to the right. Remember we decided to move the ship only a single pixel
at a time because moving the player in finer increments at higher frame
rates produces smoother animation than discontinuous jumps at slow frame
rates. The ship's overall velocity is the same, but the ship doesn't
strobe as it moves.
The screen has a wraparound feature in this game. This means that when
a ship reaches the right side of the screen and exits, it reappears on the
left side with its velocity and direction the same. This is true in the
vertical direction, too. A ship leaving the top of the screen will
reappear at the bottom. All that is needed is a simple check to determine
if the ship has reached the screen boundary. If it has, its position is
reset to the opposite screen boundary. Since the boundaries of the
playfield screen don't quite reach the edges of the television set, we
extended the screen boundary coordinates by eight pixels in all
directions. The ship's vanishing point should be nearly at the edge. If a
ship is traveling to the right, it will vanish at X = 216 ($D8) and
reappear at X = 40 ($28). Don't confuse playermissile coordinates with the
screen coordinates used in PLOT and DRAWTO statements. The top left corner
of the playfield in player-missile coordinates is X = 48, Y = 32.
Coordinate 0,0 is offscreen.
Missile MovementThe missiles in this game are controlled entirely
by a separate subroutine. The subroutine needs only the player number
inputted in the X register to operate correctly. It decides if a new
missile can be fired or if one is already on the screen, then moves the
missiles appropriately. There is no need to read a joystick for missile
direction as in our earlier game, because the missile fires and moves in
the direction, DIR, that our ship faces. Also we don't need to worry about
updating the ship's position while in the missile subroutine, since the
main program loop takes care of this.
The subroutine's initial decision is whether the joystick trigger
STRIG0,X ($284,X) is being pressed. When the button is pressed, the
subroutine returns a zero, and, if untouched, a one. There are also timers
TMIS,X for each missile, to count the number of screen cycles that a
missile travels. The actual values are unimportant, except whether they
are zero or not. When TMIS,X is greater than zero, the missile is already
on the screen and merely has to be moved while checking for screen edge
boundaries. However, if TMIS,X is zero, the missile has to be placed
initially at the ship's position, and the firing sound started.
Since we only have one missile per player, we can't have rapid fire
missiles or more than one missile on the screen at a time. Games that
allow a train of five or six missile tracks on the screen at one time are
using character set animation or bit mapping, not missiles. We could have
allowed the player to reset his missile track each time he pressed the
trigger, but instead we decided that you couldn't refire until the missile
reached the screen's edge or hit its target. Since many players might hold
the trigger down indefinitely we had to test in both branches for whether
the missile was already on the screen. If we had omitted this test, the
missile track would reset each time a player pressed the trigger. If you
wish to change the game to this mode of firing, just remove the test.
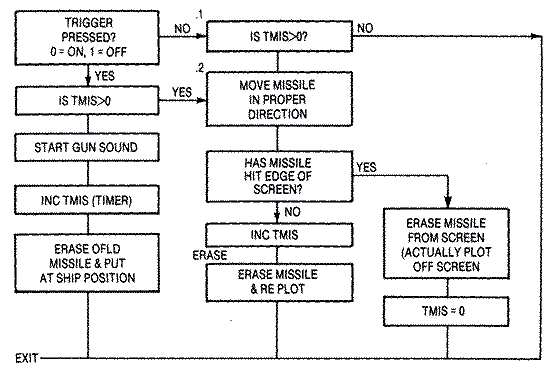
Once a missile is launched, it must continue to move in the initial
direction, regardless of a change in course of the mother ship. We
accomplish this by storing its initial direction at launch DIR,X as
DIRMO,X. This direction is used to look up the missile velocity vectors
VTX and VTY from tables. The position is updated by the following formula:
XMIS(new) = XMIS(old)+VTX(DIRM0)
YMIS(new) = YMIS(old)+VTY(DIRM0)
The code is as follows: .2 LDY DIRMO,X ;LOAD Y REG. WITH MISSILE'S DIRECTION
LDA VTX,Y ;LOOK UP X DIRECTION VELOCITY VECTOR
ASL ;DOUBLE VELOCITY VECTOR
CLC
ADC XMISO,X ;ADD MISSILE'S OLD X POSITION
STA XMISO,X ;STORE NEW X POSITION
LDA VTY,Y ;LOOK UP Y DIRECTION VELOCITY VECTOR
ASL
CLC
ADC YMISO,X ;ADD MISSILE'S OLD Y POSITION
STA XMISO,X ;STORE NEW Y POSITION
These missile shapes are not the square 2 by 2 blocks of our earlier
example. They are two pixels set vertically, horizontally, or diagonally
in the direction of travel. A chart of their shapes follows:
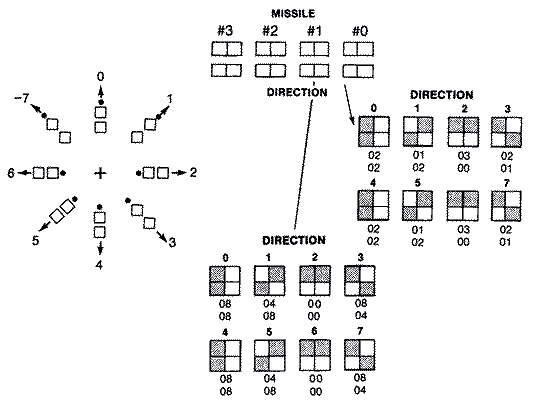
First, notice that each missile has a different set of numerical
values. Missile shape #0 uses the first two bits in the byte, and missile
#1 uses the third and fourth bit positions. Therefore, there is a shape
table for each missile. The shapes are stored in two-byte pairs for the
two scan line high shapes. There is also an index to the low byte to each
of these shapes. They are in two tables called MISLO and MISLO1 for each
missile set respectively.
The missile setup subroutine sets up the zero page pointers to the
correct shape and to the storage location in player-missile memory. This
area is just below the players or.75K from the start of player-missile
memory. In addition, the proper mask for that player is stored as MASK,
Plotting the missile requires erasing the old missile first by ANDing
the byte containing all four missiles with the proper mask. This step
erases only the desired missile because the mask contains zeros in the
missile bits to be erased and ones elsewhere. We then plot the missile on
the screen by ORAing with a byte in the missile memory that may or may not
contain other missiles. For example, if we wish to erase missile #I in a
byte that contains missile #0, we AND it with the mask $FC. 00001010 MEMORY
AND 11111000 MASK
00000110 RESULT
If we move missile #1 to a scan line that contains missile #3 then we
ORA its shape with the byte in missile memory for that scan line. 00000100 MEMORY
ORA 00000010 SHAPE
00001000 RESULT
s
The code is shown below: MPLOT LDY #$00
.1 LDA (SHPMOL),Y;LOAD OLD SHAPE
AND MASK ;MASK WITH PROPER MISSILE BEING MOVED
STA (SHPMOL),Y;STORING IT DOESN'T ERASE OTHER MISSILES
INY ;NEXT BYTE
CPY #$02 ;MISSILE 2 BYTES HIGH
BLT .1
LDY #$00
.2 LDA (SHPL),Y ;GET BYTE FROM CORRECT SHAPE TABLE
ORA (SHPML),Y ;ORA AGAINST OTHER MISSILES ON SCAN LINE
STA (SHPML),Y ;PUT IN MISSILE AREA
INY ;NEXT BYTE
CPY #$02
BLT .2
Derez Style ExplosionThere are many types of explosions suitable
for destroying a killed spaceship. One of the more effective methods is to
de-rez the object. This technique makes the object appear to slowly
disintegrate by randomly flickering the individual pixels until most of
the pixels vanish.
The trick is to take the ship and store it into a temporary shape table
called DEREZ. We load a random number, then ORA it with another random
number to insure that we don't get a number with a few of bits "on". We
then AND it with the shape in DEREZ and store it there. If we then AND the
original ship's shape with this value three times, we get a significantly
degraded image of the ship. We then ORA this with our degraded temporary
shape in DEREZ so that we get a less degraded shape than we would get if
we performed only the first of the two previous steps. Since we wanted
this effect to last at least 30 cycles or half a second, the routine was
largely experimentally determined. The image begins to degrade slightly
during each cycle but isn't quite steady. Any byte's image can improve
slightly but randomly in any frame, but the overall effect is continued
degradation. The loop is 48 cycles but the image usually vanishes
completely after 30 cycles. An example of two separate passes for a single
byte is shown below.
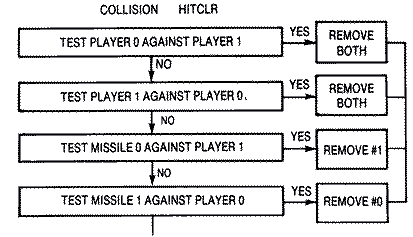
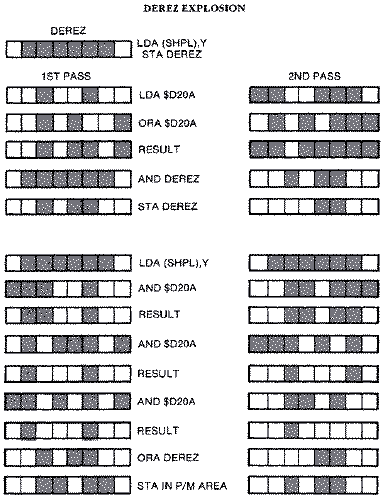
The explosion sound gives the effect of a slow rumble that slowly
decreases in volume. We are working with a fairly low frequency and a
distortion of zero in channel one and a distortion of 8 in channel 2. The
use of two channels with these distortion and frequency values was
determined experimentally to produce the best effect. ORing SBANG/4 with
$E0 gives us a range of frequencies $EO-$EF. These are stored in AUDF1 and
AUDF2. Since both AUDCI and AUDC2 use the lower nibble for volume control,
the value for AUDC1 can be obtained by ANDing the frequency with #$OF to
mask out $EO. Since the upper nibble is the distortion, then a distortion
of 8 can be obtained in AUDC2 by ORing AUDCl with #$80. The equivalent
sound routine in BASIC is as follows: 10 FOR SBANG=64 TO 0 STEP -1
20 X=INT(SBANG/4)
30 SOUND 0,224+X,0,X
40 SOUND 1,224+X,8,X
50 NEXT SBANG
ScorekeepingThe score line is Written directly into GRAPHICS 1
(ANTIC 2) playfield memory beginning at the top of the screen memory.
These locations SCREEN to SCREEN+ 19 contain internal character code
valves stored initially in a table called SCLINE. During initialization
they are moved into screen memory and the scoring digits, SCREEN+7,
SCREEN+8 (tens digit, ones digit) for ship #0 and SCREEN+18, SCREEN+19
(tens digit, one's digit) for ship #1 are updated during the game. A
diagram showing the score line and its internal character data is
illustrated below.
Flow Chart & Game Code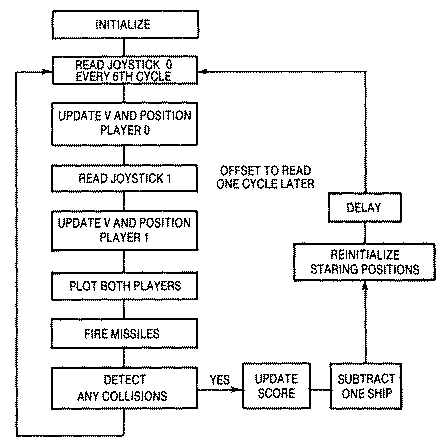
<
Download
SPACEWAR.EXE (Executable program)
Download
SPACEWAR.OBJ (Object code)
Download
/ View
SPACEWAR.LST (Assembler listing)
Download
/ View
SPACEWAR.S (Source file)
Download
/ View
SPACEWAR.RAW (As printed in book)
Player Missile EditorWe have included a player-missile editor
that will make designing player shapes easy. The grid on the left hand
side of the screen supports a shape twenty-two scan lines high in the
single-resolution mode. Each of the enlarged blocks is the same shape as
the individual pixels on the screen.
The cursor appears in the upper left hand corner. The message at the
upper right initially is set in the NOPLOT mode. To put the cursor in the
PLOT mode, press the letter P, for the ERASE mode, press the letter E, or
return to the NOPLOT mode by pressing N. Pressing any of the arrow keys
without the control key moves the cursor. Move the cursor to your desired
starting position, and press P for plot. A block fills for each position
of the shape, and the byte's decimal and hexadecimal value appears to the
side.
As your shape forms, you will begin to see an actual sized player shape
emerge in the lower right portion of the screen. You can toggle the player
width by pressing the W key. It will progress from single width to double
width to quadruple width before returning to single width. Likewise,
toggle the player resolution from singleline resolution to double-line
resolution by pressing the R key. If you wish to clear the entire screen
of your shape, just press SHIFT-CLEAR.
The editor, which is written in BASIC, is somewhat slow. Most of its
slowness is due to our decision to write it in graphics mode 8, so that we
could plot accurately while simutaneously incorporating text on the
screen. Machine language programmers need the hexadecimal values of the
player shapes for their shape tables. Owners of the ABC BASIC compiler by
Monarch Data Systems will find that the program compiles with no
modification, and runs significantly faster.

&&&
Player-Missile Movement Using Strings
An alternate method of moving player shapes vertically at close to
Machine language speed is to take advantage of Atari BASIC's string
manipulation routines. One in particular in the form of PO$(N)=SO$ will
take a smaller string such as S0$="ABCD" and place it starting at the Nth
position of the larger string P0$. Thus, if N=6, P0$ would be as follows: BYTE VALUE
1 0
2 0
3 0
4 0
5 0
6 ASCII A
7 ASCII B
8 ASCII C
9 ASCII D
10 0
11 0
The shorter string could just as easily be our player shape. It would
be very easy to move it just by changing the value of N. The only hitch is
that we would have to erase its previous position before we moved it, or
the player string would begin to repeat itself, or parts of itself, within
the larger (256 byte) player area string. Since there is no need to move
the player more than two bytes at a time, we can easily accomplish the
erase by overwriting the trailing or leading edge of our last position
with two trailing null or zero characters at each end.
How BASIC Stores StringsThe biggest problem in this method is -to
fool Atari BASIC into assigning the player-missile display area as a
string variable. In order to understand how to do this, it is necessary to
know how Atari BASIC stores variables in memory. Two areas are set aside
in memory. The first, the Variable Value Table Pointer (VVTP), stores
eight bytes of information for each variable declared in your BASIC
program. The second, the String Array Table, reserves space in memory
according to the size specified when you dimension an array. The VVTP
table is arranged as in the following example. If it were for a string
dimensioned as P0$(255) it would have these values:
Every time BASIC has to access information in a string it goes to the
VVPT to find the current address of the string. Byte I contains the
variable type which is 129 for a string. Byte 2 contains the variable
number. BASIC tokenizes variables and refers to them by numbers, not
names. Bytes 3 and 4 contain the value of the offset from the string/array
area (STARP) where BASIC reserves memory for all dimensioned variables.
The values are in low byte, high byte order. Thus the address of your
string is STARP + Byte 3 + 256*Byte 4.
If we change the pointers to bytes 3 and 4 so that they now point to
the playermissile area for player #0, we could use string move commands to
move our player. To do this we will need to calculate the difference
between the player-missile area and where BASIC was planning to store our
string in STARP.
VVTP= PEEK(134) + 256*PEEK(135)
STARP = PEEK(140) + 256*PEEK(141)
PLAYER0 =PMBASE*256 + 1024
so
OFFSET=PLAYER0 - STARP
If we take this OFFSET value and divide it into its low and high byte
values, then POKE them into bytes 3 and 4, BASIC would think that our
strings were actually in the player-missile area. Since we have four
players, we have to do this for each group of eight bytes in the VVTP
table. Your dimensioned player strings should be the first variables in
the program; otherwise, you will have to scan through the table looking
for a match.
The following example uses this technique to move four players
vertically. Horizontal movement is of course done by setting the player's
horizontal position register. The example has four randomly moving,
bouncing balls which reverse direction upon collision with another ball or
the playfield boundary.
Just to give you a rough idea of the actual memory locations and the
change we need to make in the VVTP table for player #0, the values for the
examy4e are listed below:
VVTP = 7760
STARP = 10932
PMBASE = 38912 (High byte = 152)
PLAYER0 = 39936
so that OFFSET = PLAYER0-STARP = 29004 then LO = 76 and HI = 113 and
they are POKED into bytes 3 and 4 respectively.
Download
PMDEMO.BAS (Saved BASIC)
Download
/ View
PMDEMO.LST (Listed BASIC)
While this is a clever method of obtaining fast vertical motion for
players, there is no easy way to animate more than a single missile when
using strings. The technique is shown more for completeness than for
usefulness. We suggest that you use our player-missile subroutine for your
games and avoid the complications of using string manipulation.
Return to Table of
Contents | Previous
Chapter | Next Chapter
|
|



