|
Chapter 8
Raster Graphics & Sound
Raster graphics is a term we very rarely use in connection with the
Atari computer system. It is a term that describes how individual pixels
are mapped on a highresolution screen. The technique is about the only one
possible on computers such as the Apple 11 and the IBM PC. Atari
programmers like to use easier and more colorful techniques like character
graphics and playermissile animation, but there are certainly a number of
valid reasons for animating with raster graphics. The two best reasons are
that Graphics mode 8 (ANTIC mode F) screens have the highest resolution
(320 x 192 pixels), and that very large shapes can be smoothly animated.
The biggest disadvantage is that you can have shapes with three colors at
best.
Graphics 8 screens produce color by a method known as artifacting. On
computers with a GTIA chip, pixels in even columns appear blue and those
in odd columns appear green when the background color register is set to
black. Obviously, we could obtain other color combinations by varying the
background color register. If you wish to draw a shape entirely in blue,
you need only plot the shape's individual pixels in the even columns.
Similarly, you will obtain an all-green shape if you plot pixels only in
the odd columns. When a blue pixel is next to a green pixel, the pair
appears as white.
You get these alternating stripes of color because the Atari sends its
color signal as a series of square wave pulses. One complete cycle is
called a color clock. When the square wave is high you get blue, and when
it is low you get green. Other colors are produced by phase shifting the
square waves. These colors have nothing to do with the positions of the
actual phosphors on the television tube.
Pixel information is encoded eight pixels per byte. The screen is made
up of 192 rows of forty bytes. Forty bytes times eight pixels per byte
gives a horizontal resolution of 320 pixels. If you are working in color
you are really only talking about half that, or 160 pixel pairs
horizontally.
Plotting pixel data is quite anolagous to plotting character data to
the screen. In fact, if we took the character data for the letter "A" and
plotted it on the screen by calculating the byte address for a particular
column in the first eight rows, the character would appear as expected. Of
course, it is a lot of trouble to just plot character data on a Graphics 8
screen, but it only illustrates the technique.
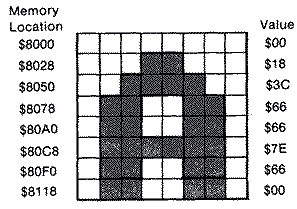
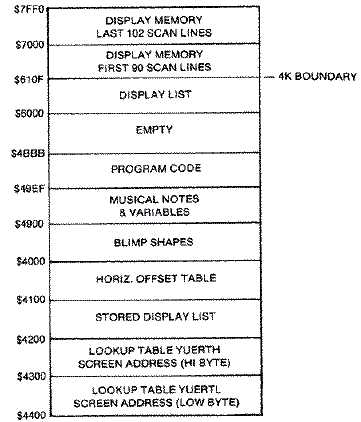
A Graphics 8 screen fortunately can be mapped sequentially in memory if
you are clever. The problem is that a display list cannot address screen
memory that crosses a 4K boundary. An additional LMS instruction is needed
on the other side of the boundary. You could fit 102 lines in the lower
portion, but that would leave a 16-byte gap between the two sections.
Instead, I decided to place 102 lines in the following example in the top
4K of screen memory and butt the first ninety lines against it in the
lower 4K section. This leaves 496 bytes of free memory at the beginning
and ample room to place the display list. The display list begins at
$6000, and screen memory at $61F0. The 0th or top line starts at that
address and the first line begins forty bytes later at $6218. Each of the
192 lines is offset in memory by an additional 40 bytes.
To plot a byte at a particular X,Y coordinate on the screen requires
you to calculate a memory address based on the starting address of the row
and the offset into the row. The formula is:
MEMORY ADDRESS = SCREEN MEMORY +(Y*40)+(X/8)
It isn't a difficult calculation, except that in Machine language,
multiplication and division other than by multiples of eight require an
enormous number of steps. If you only had to do it once, it would be
alright. Unfortunately, you need to perform the calculation at least once
for each row of the shape. If you were trying to do a Galaxian-type game
where you had several dozen shapes, you would never have enough time to
move and draw them all and achieve a fast enough animation frame rate. A
better method is to look up the starting address of the row from a table
and just calculate the horizontal offset based on the shape's Y
coordinate.
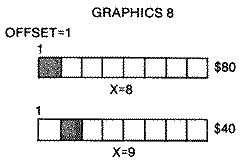
Plotting a pixel on the screen at a particular X,Y coordinate, based on
its row and horizontal offset, will work only if the Y coordinate was a
multiple of eight. The pixel would be physically at the left end of the
byte and would have a value of $FO. If you want to plot a pixel one unit
further to the right, you need a byte with an entirely different pixel
pattern. You can't physically move the byte just anywhere, like a "tad" to
the right. The value of that byte is $80. Now, you begin to realize that
you need eight different bytes just to cover all of the possible X
coordinates. Since this is also true of larger shapes, we have a difficult
problem.
Color shapes have another problem. If you move them right or left one
pixel, they shift colors. Therefore, you must move them two pixels left or
right at a time. While this sounds complicated, it actually reduces the
number of shifted shape tables to four. It has one additional advantage in
that there are only 160 possible horizontal positions instead of 320. This
reduces the arithmetic to single-byte operations.
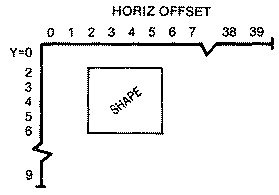
Bit Mapping the ShapesDrawing a bit-mapped shape table anywhere
on the Graphics 8 screen is a simple procedure, once you understand the
basic concept. The shape table is stored sequentially in memory, either by
rows or columns. The technique, therefore, is to load each of these bytes,
one at a time, into the Accumulator, find the position in memory for the
screen location where you want to plot that byte, then store it in that
location.
Memory Location by Table LookupThe difficulty, as we showed
earlier, lies in finding a particular memory location, given an X,Y screen
coordinate. Table look-up is obviously the fastest method for finding the
starting address for the first position (leftmost) or 0th offset for each
of the 192 lines. If the screen started at $61F0, the first line or line
#0 would begin at this address, and the second line would begin at $6218.
Each address takes two bytes. The first part is the high byte which in the
latter case is $62. The second part, $18, is the low byte. These values
can be separated into two tables, one containing the lower order address
of each line (call it YVERTL), and the other containing the higher order
address of each line (call it YVERTH). Each table is 192 bytes long
(0-191). In order that these tables not become specific to a particular
screen address, the values are merely offset values from a zero starting
address. The GETADR subroutine adds the high byte of the starting screen
address to obtain a specific memory address. Our only constraint is that
the screen start on a page boundary.
You can access any element in either table by absolute indexed
addressing. The effective address of the operand is computed by adding the
contents of the Y register to the address of the instruction. The format
is:
EFFECTIVE ADDRESS = ABSOLUTE ADDRESS + Y REGISTER
If our YVERTL table were stored at $4000 and we wanted to find the
starting address of line I (remember lines are numbered 0-191), we would
index into the table one position and load that value into the
Accumulator.
4000:F0 18 40 68 90 B8 ..... YVERTL TABLE
So LDA YVERTL,Y, where the Y register =$01, will fetch the value $18
from memory location $4000 + $01 = $4001, and place it in the Accumulator.
Similarly, if YVERTH were stored in the next page following our first
table, then:
4100:01 02 02 02 02 02 ..... YVERTH TABLE
If the Y register = $01, then a LDA YVERTL,Y will take the value $02
stored in memory location $4100 + $01 = $4101, and place it in the
Accumulator.
Storing the Shape in Screen MemoryEventually we will want to
store the first byte from the shape table into a memory location. This can
be done efficiently if the two-byte address is stored sequentially in zero
page. Let's store the low-byte half of the address, HIRESL, at location
$F2, and the high-byte half, HIRESH, at location $F3 in zero page: LDY #$01 ;Y REGISTER CONTAINS LINE
LDA YVERTH,Y ;LOOKUP HIGH BYTE OF START
;OF ROW IN MEMORY
STA HIRESH ;STORE IN ZERO PAGE OF MEMORY
LDA YVERTL,Y ;LOOKUP LOW BYE OF ROW IN MEMORY
STA HIRESL ;STORE IN ZERO PAGE OF MEMORY
If the computer finds a $00 in location $F2 (HIRESL) and a $60 in
location $F3 (HIRESH), then the base address is $6000. The Accumulator
stores a value into memory location $60000+$01, or lacation #6001, as
shown on the following page.
The final addressing mode that we must consider is Indexed Indirect
Addressing. The format is:
LDA (SHPL,X)
It is very similar to the Indirect Indexed addressing mode except the
index is added to the zero page base address before it retrieves the
effective address. Its primary use is to index a table of effective
addresses stored in zero page, but in the form we are going to use it, the
X register is set to 0. Thus, it simply finds the base address.
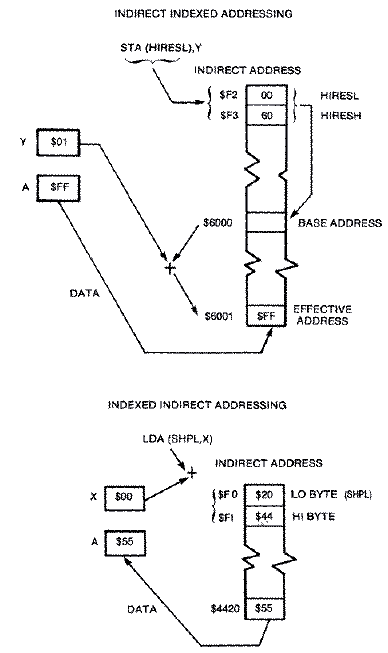
We must use this second form of indirect addressing because there is a
shortage of registers in the 6502 microprocessor. We are already using the
Y register in the store operation, and there isn't an indirect indexed
addressing mode of the form LDA(SHPL),X. Thus, we must go to the
alternative addressing mode LDA(SHPL,X).
What this all boils down to is that we want to load a byte from a shape
table into the Accumulator and store it on the screen with the following
instructions: LDA (SHPL,X) ;LOAD BYTE FROM SHAPE TABLE
STA (HIRESL),Y ;STORE BYTE ON HI-RES SCREEN
We can index into the shape table by incrementing the low byte SHPL by
one each time, then store that byte into the next screen position on a
particular line by incrementing the Y register. This zero page method is
faster than performing the equivalent code with absolute index addressing,
because twobyte addresses can be handled with fewer instructions, fewer
machine cycles, and less memory space.
Obviously, a generalized subroutine must be developed to find the
screen memory address (HIRESL and HIRESH), given a line number and a
horizontal displacement. We will call this subroutine GETADR, short for
Get Address.
Each time a row of shape-table bytes is transferred to succesive memory
locations in screen memory, the program will call the subroutine GETADR.
The line's starting memory address is then offset by the horizontal
location of the shape on the screen. Our table of line addresses is only
an offset, so it will need to add the actual starting address of the
screen.
Memory address = Line # starting address + horizontal offset GETADR LDA YVERTL,Y ;LOOKUP LOW BYTE ADDRESS OF LINE
CLC
ADC HORIZ ;ADD HORIZ. OFFSET
STA HIRESL ;STORE LOW BYTE OF SCREEN ADDRESS
LDA YVERTH,Y ;LOOKUP HIGH BYTE ADDRESS OF LINE
ADC /SCREEN ;ADD HIGH BYTE OF SCREEN ADDRESS
STA HIRESH ;STORE HIGH BYTE SCREEN ADDRESS
RTS
where the Y register has a vertical screen value (0-191).
If you are designing an arcade game, you will probably have several
different shapes on the screen at one time. Keeping track of each shape's
variables, which are inputted into a generalized drawing routine, is
generally easier if a set-up routine is incorporated into your program.
This assures that you haven't forgotten to initialize anything before
entering the drawing routine. Only a few variables need to be defined in
the set-up routine: the location of the shape table; the horizontal
displacement on the screen; and the width and depth of the shape.
The drawing routine becomes more efficient the fewer times it accesses
the GETADR subroutine. Therefore, it is much faster to load and store on
the same screen line until the end of the shape's width is reached.
Drawing our balloon a byte at a time across its width will only require
calling GETADR 31 times. But if we plotted down instead, GETADR would be
called for each byte, or 279 times, an unnecessary waste of time.
As we load and store across a particular screen line, we decrement
SLNGH, the ship's width, until SLNGH equals zero. When we are finished
with a row, we increment TVERT to the next screen line down and decrement
the DEPTH. When DEPTH reaches zero, we have plotted all rows of the shape
and we are finished. DRAW LDY VERT ;VERTICAL POSITION
JSR GETADR ;FIND BEGINNING OF SCREEN ADDRESS ROW
LDX #$00
LDA TEMP
STA SLNGH ;RESTORE VALUE OF WIDTH FOR NEXT ROW
LDY #$00
DRAW2 LDA (SHPL,X) ;GET BYTE OF SHAPE TABLE
STA (HIRESL),Y ;PLOT ON SCREEN
INC SHPL;NEXT BYTE OF SHAPE TABLE
BNE .1 ;IF CROSS PAGE BOUNDARY?
INC SHPH ;INCREMENT TO NEXT PAGE OF SHAPE
.1 INY ;NEXT POSITION ON SCREEN
DEC SLNGH ;DECREMENT WIDTH
BNE DRAW2 ;FINISHED WITH ROW YET?
INC VERT ;IF SO, INCREMENT TO NEXT LINE
DEC DEPTH ;DECREMENT DEPTH
BNE DRAW ;FINISHED ALL ROWS?
RTS ;YES, END
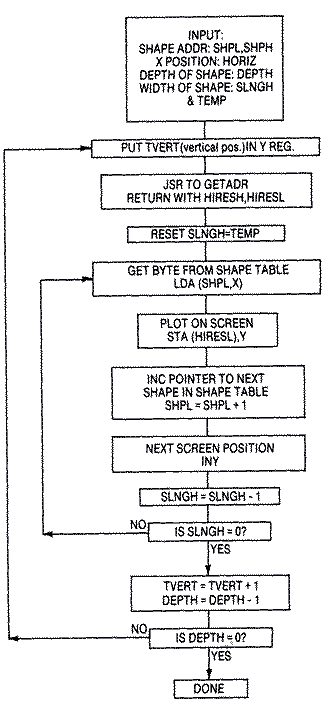
Although the first row of the shape can be plotted at any VERT (0-191)
position, if VERT began at 190, the computer would attempt to plot the
third line at VERT=192. Indexing into the table that far would most likely
produce garbage, as you would index beyond the end of the table. You
should always be careful that:
TVERT <= 192-DEPTH
A simple test somewhere before the draw subroutine would suffice, but
it might be incorporated into your joystick read routine.
XDrawing ShapesObjects that move on the screen are shifted in
position by erasing the object's first position before drawing it at its
new position. The simplest method is to draw the shape by Exclusive-ORing
it before shifting it.
EOR InstructionThe Exclusive-OR instruction, EOR, is primarily
used to determine which bits differ between two operands, but it can also
be used to complement selected Accumulator bits. The way it works is
elementary. If neither of two particular memory bits is set or their
values are zero, the result is zero. If either one is set, then the result
is one. But if both are set, they cancel and the result is zero. MEMORY BIT ACCUMULATOR RESULT BIT IN
BIT ACCUMULATOR
0 0 0
EOR 0 1 1
1 0 1
1 1 0
If we take a byte on the screen and EOR it with the same byte 0 1 1 0 0 1 1 0 SHAPE ON SCREEN
0 1 1 0 0 1 1 0 SHAPE
_______________
0 0 0 0 0 0 0 0 RESULT
From the shape table, the result is zero or a screen erase. A similar
effect would occur if a blank screen were EORed with a shape, then EORed
again. 0 0 0 0 0 0 0 0 BLANK SCREEN
EOR 0 1 1 0 0 1 1 0 WITH SHAPE
_______________
0 1 1 0 0 1 1 0 RESULT IS SHAPE ON SCREEN
EOR 0 1 1 0 0 1 1 0
_______________
0 0 0 0 0 0 0 0 RESULT IS BLANK SCREEN
It doesn't damage the background if a shape is EORed on the screen,
and then off again. However it does distort the shape slightly. 0 0 0 0 0 0 0 1 BACKGROUND
EOR 0 0 1 0 1 1 0 0 WITH SHAPE
_______________
0 0 1 0 1 1 0 1 RESULT ON SCREEN (SHAPE
DISTORTED LAST BIT)
EOR 0 0 1 0 1 1 0 0 WITH SHAPE
_______________
0 0 0 0 0 0 0 1 GET BACKGROUND BACK
In the above example, an extra pixel in the shape's last bit
position distorts the shape drawn on the screen. In the example below, the
fourth bit position becomes a hole in the shape. 0 0 0 1 0 0 0 0 BACKGROUND
EOR 0 1 0 1 1 0 0 0 WITH SHAPE
_______________
0 1 0 0 1 0 0 0 RESULT ON SCREEN
^---------hole here
EOR 0 1 0 1 1 0 0 0 WITH SHAPE
_______________
0 0 0 1 0 0 0 0
There are some techniques to avoid distorting the shape when the
background is likely to interfere during the drawing process. This
involves a combination of EORing and ORing the screen with the background
stored in an alternate screen memory. An alternate method is to store the
screen memory bytes in a temporary table equal in size to your shape,
while you draw your shape. When erasing, you replace the shape with the
background stored in your temporary table.
OR InstructionThe OR memory with Accumulator (ORA) instruction
differs from the EOR instruction in that if both memory and Accumulator
bits are on, then the result is one, or on. MEMORY BIT ACCUMULATOR RESULT BIT IN
BIT ACCUMULATOR
0 0 0
ORA 0 1 1
1 0 1
1 1 1
If the background were as follows, and you ORed it with the shape,
the shape remains correct. 0 0 1 0 1 0 1 0 BACKGROUND
ORA 0 1 1 1 1 0 0 0 WITH SHAPE
_______________
0 1 1 1 1 0 1 0 GET SHAPE + BACKGROUND WITH NO HOLE IN SHAPE
Unfortunately, if you EOR this result with the shape again, the
background is flawed. 0 1 1 1 1 0 1 0 SHAPE + BACKGROUND
EOR 0 1 1 1 1 0 0 0 WITH SHAPE
_______________
0 0 0 0 0 0 1 0 FLAWED BACKGROUND
We can incorporate the Exclusive-OR instruction in our XDRAW
routine. If we EOR the shape we had previously on the screen, nothing
remains. 00010 XDRAW LDY TVERT ;VERTICAL POSITION
00020 JSR GETADR
00030 LDA TEMP
00040 STA SLNGH ;RESTORE VALUE OF WIDTH FOR NEXT ROW
00050 LDX #$00
00060 XDRAW2 LDA (SHPL,X) ;GET BYTE FROM SHAPE TABLE
00070 EOR (HIRESL),Y ;EOR WITH BYTE ALREADY ON SCREEN
00080 STA (HIRESL),Y ;DRAW ON SCREEN
00090 INC SHPL ;NEXT BYTE OF SHAPE TABLE
00100 INY
00110 DEC SLNGH ;DECREMENT WIDTH
00120 BNE DRAW2 ;FINISHED WITH ROW?
00130 INC TVERT ;IF SO, INCREMENT TO NEXT LINE
00140 DEC DEPTH ;DECREMENT DEPTH
00150 BNE DRAW ;FINISHED ALL ROWS?
00160 RTS ;YES, END ROUTINE
Now that we know how to DRAW and XDRAW a bit-mapped shape anywhere
on a Graphics mode 8 screen, the principle for animating them is simple. A
shape is erased from the screen, its new position is calculated, then it
is redrawn at its new position. The procedure is outlined below.
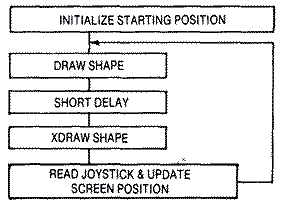
A delay has been inserted between the DRAW and the XDRAW to allow the
object to be on the screen longer than it is off. Without the delay, the
object is erased immediately after it is drawn. This does not give the
shape's image sufficient time to remain onscreen during one animation
frame. The result is a badly-flickering image. A small delay can be
inserted by checking the internal clock at $14 for so many jiffies.
Experiments show that 3/60 seconds is a good value.
Whenever a shape is moved horizontally, the bit pattern within a screen
memory byte shifts and sometimes even intrudes into the adjacent byte. To
avoid color shifts due to the odd-even column artifacting, shapes must be
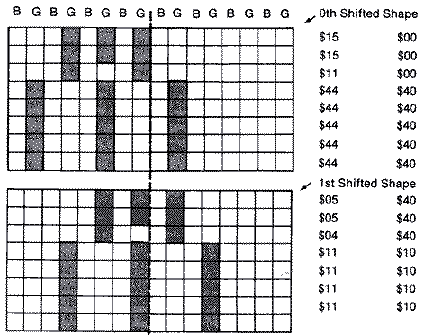
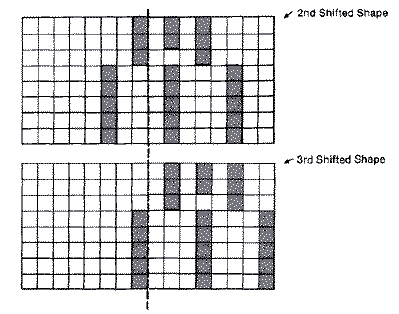
moved horizontally two columns at a time. If we consider the
four-pixel-wide shape in the diagram below and move it right two bits at a
time, it retains the same shape and color pattern, but the value in its
shape table changes. If we shift the shape far enough, some of the bits
run into the next byte. By the time we have shifted it the fourth time,
the pattern repeats itself as if it were in the same starting position but
one byte over. So if we are going to be able to move a shape anywhere on
the screen, we will need four shifted shape tables each one byte wider
than the original shape. And since we need to move the shape horizontally
two pixels or color clocks at a time, it would be easier to work with a
coordinate system that goes from 0-159 instead of 0-319.
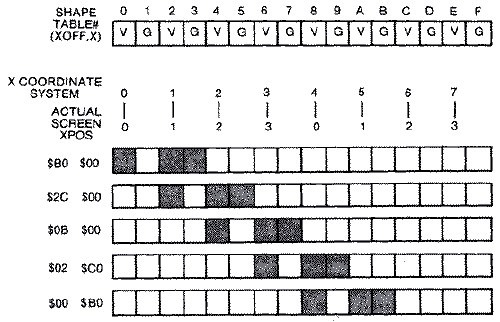
It would be nice if there were a relationship between the horizontal
position (X) and the shape #. The mathematical relationship is as follows:
TEMP = INT (X/4)
SHAPE# = X-TEMP*4
Actually, it is a lot faster to look the value up in a table called
XOFF. This table has the shape table # for each possible X position. You
can retrieve the shape table number by indirectly indexing into the table
with the X position in the Y-register. We use another small table SHPLO to
store the low byte starting positions of each of the shape tables, and
another called SHPHI if the combined length of the four shapes crosses a
page boundary. The code to set up the pointers to the proper shape is as
follows: LDY X ;HORIZONTAL POSITION (0-159)
LDX XOFF,Y ;INDEX TO FIND SHAPE #
LDA SHPLO,X ;INDEX TO GET LOW BYTE OF SHAPE TABLE
STA SHPL ;STORE LOW BYTE IN ZERO PAGE
LDA SHPHI,X ;GET HIGH BYTE OF SHAPE TABLE
STA SHPH ;STORE HIGH BYTE IN ZERO PAGE
The drawing routine is exactly the one described earlier. Once the
pointers to the proper shape table are inputted with both the shape's
vertical position and horizontal offset, bytes can be transferred to
screen memory from the appropriate shape table.
The XDRAW subroutine differs from our drawing routine in only one
instruction. Instead of just fetching a byte from our shape table and
placing it directly in screen memory, this routine EORs it with the byte
already on the screen before storing it there. The bits are effectively
erased if the screen image byte and the shape table byte are a match. LDA (SHPL,X) ;GET BYTE FROM SHAPE TABLE
EOR (HIRESL),Y ;EOR WITH SCREEN IMAGE
STA (HIRESL),Y ;PLOT ON SCREEN
Collision DetectionDetecting collisions between raster shapes
isn't easy. There aren't any collision registers to query as you can when
working with player-missile shapes. Instead, when drawing the shape, you
must simultaneously test for any other pixels within that byte's (or
pixel's) screen location. The test is performed using the AND instruction.
The AND InstructionThe truth table for the AND instruction is as
follows: ACC. MEMORY RESULT
0 0 0
0 1 0
1 0 0
1 1 1
Both Accumulator and memory must be on (set) for the result to be on
(set).
If we take a screen memory location that has an object in it and AND it
with a byte from our shape table, any duplication in any bit location
where something is already on the screen will give a non-zero result. 0 1 1 1 1 0 0 0 Background
AND 0 0 0 1 1 1 1 1 Shape
_______________
0 0 0 1 1 0 0 0 Result $18 >Zero
Drawing While Testing for CollisionUsually, in any game, if a
collision is detected, the object is to be removed. Your first instinct is
to stop drawing the object since it is to be removed anyway. But if you
are Exclusive-ORing (EORing) the screen and you stop in the middle of your
shape, you are going to leave a mess. It is much better to set a collision
flag, finish drawing the shape, then remove the object later by completely
EORing the shape off the screen. LDA (SHPL,X) ;GET BYTE FROM SHAPE TABLE
AND (HIRESL),Y ;AND WITH SCREEN IMAGE
BEQ DRAW ;BRANCH ON NO COLLISION
LDA #$01 ;SET COLLISION FLAG
STA ESET
DRAW LDA (SHPL,X) ;GET BYTE FROM SHAPE TABLE
EOR (HIRESL),Y ;EOR WITH SCREEN IMAGE
STA (HIRESQ,Y ;PLOT ON SCREEN
Collision Detection - A Special CaseAny two objects of byte size
or larger should have no problem with collision detection, especially if
you are working with solid white objects. But there is a specific case
involving artifacting in which collision detection would not work. Let us
assume that we have a blue spaceship and a green alien that appear to
collide. If ,we examine their bit patterns, you will notice that they
never coincide. B G B G B G B G B G B G
_______________________
0 0 1 0 1 0 1 0 1 0 1 0 SHIP
AND 0 0 0 1 0 1 0 1 0 1 0 0 ALIEN
_______________________
0 0 0 0 0 0 0 0 0 0 0 0 RESULT O
The solution is to test the ship against screen memory with what is
called a "mask" of the ship's shape, as if the ship were solid white. We
take this mask of the ship, which has both blue and green pixels lit, and
AND it against the alien occupying the same screen locations. A collision
will be detected in this case. We set a flag, and then take the
appropriate byte from the blue ship's shape table and EOR it against the
screen.
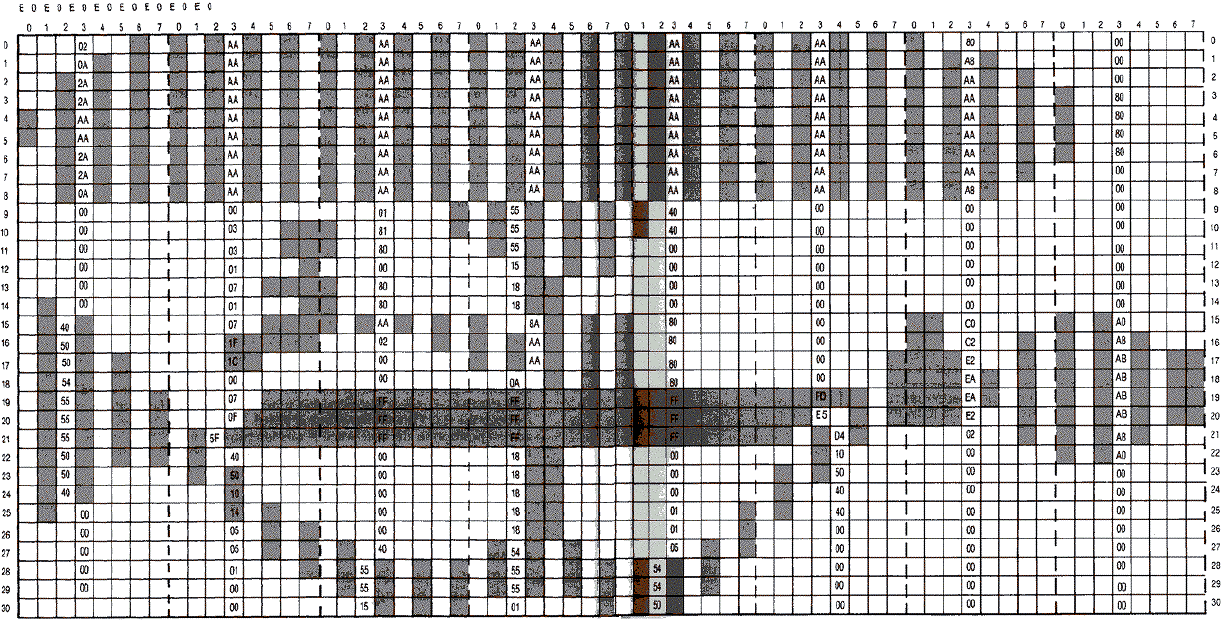
Blimp ExampleA good raster graphics example would be one that
would be difficult or impossible to do with either animated character
graphics or player-missile graphics. The large elongated blimp shape in
this example is eight bytes wide (nine if you count the byte needed for
the offset shapes), and thirty-one scan lines deep. By artifacting, we are
able to produce a shape of three different colors: blue, green, and white.
The shape is outlined below.
The blimp is joys tick-con trolled and therefore free to move anywhere
on the screen. You have to be very careful that you don't try to plot the
shape beyond the screen boundaries. While plotting bytes beyond the right
edge would produce a wraparound effect at the left edge one scan line
lower, plotting beyond scan line 191 could create severe problems by
wiping out some portion of memory. If we exceed the bounds of our YVERTL,
YVERTH tables, unknown pointers to our plotting position in screen memory
would be placed in zero page. In this case, the vertical position cannot
exceed 192-31 = 161. All of these tests are incorporated in the joystick
subroutine.
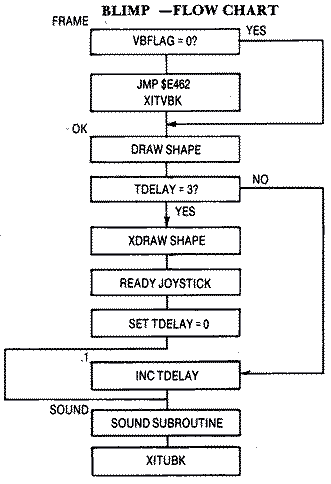
Flickering Problem with Large Raster ShapesThe first time we
attempted the example, we placed the raster drawing code outside of VBlank
and the music routine in VBlank. Unfortunately, the rastered image
flickered badly because the image, after remaining on the screen for
several frames, has to be erased at some point before it is redrawn at its
new position. Since this takes place when the electron beam is on the
screen, there is a slight gap, possibly as long as a frame, before the
redrawn image is in place. This never seems to be a problem on other
computers like the Apple 11, but then they use interlacing techniques to
produce their television images while the Atari does not.
We then felt that the animation should become flicker-free if we moved
the raster drawing routines inside VBlank. This way the rastered image
could be erased and redrawn while the electron beam was mostly off-screen.
We arranged the code so that the shape is drawn initially, remains
stationary on the screen for three television frames, then is erased,
moved, and redrawn on the fourth frame. A timer called TDELAY is set to
zero after each erasure, and increments with each frame. A test will cause
a branch past the erase-moveredraw code when TDELAY is not equal to three.
When it is equal, it will erase the shape, read the joystick, calculate
its new position, then redraw it in that position.
We feared that the code might be too long to fit within one Deferred
VBlank cycle because the shape was nine bytes by thirty-one scan lines.
Having never encountered the problem before, I became confused with the
buggy results. The code was arranged differently within the Vblank at the
time. The sound routine was last, and I was drawing the raster shape on
each frame. The routine invariably drew the shape then hung the first time
it was run after assembly, but would actually execute the code after a
system reset. A more serious problem was that six complete scan lines
directly beneath the shape were garbaged. The routines worked when the
code was outside VBlank.
Testing Whether Code Finishes Before VBlank EndsAfter many wasted
hours, we decided that a test would be needed to determine if and when the
end of the VBlank code was ever reached. Obviously, if we reached the end
we wouldn't have a problem; however, if we didn't, we would have to finish
it on the next cycle. Let's assume that we haven't finished it when the
computer says it's time for a new VBlank Interrupt to occur. It saves all
of the registers and its position within the code just like it was outside
VBlank. Now when a new VBlank Interrupt occurs, it begins again from the
top. Fine, it executes the sound routine but when it tests if VBFLAG = 0,
it discovers that it never finished the last VBlank and exits through the
exit VBlank subroutine at $E462. The computer restores the registers and
its position in the code when it was interrupted. It then finishes the
VBlank routine. While this is a good example of how to correct the problem
of VBlank routines that are too long, it fails to completely smooth out
the animation. However, it is slightly better than when the raster code
was completely outside VBlank.
If you would like to observe what happens if the above method isn't
incorporated within your program, try removing the JMP $E462 statement.
The result is a screen that has gone wacko. The rastered shape is plotted
in pieces on different scan lines, and the display begins to roll.
Background SoundThe background sound throughout our raster
example is a familiar tune. The sound routine, which is explained in the
next section, reads the individual notes and their length from a table. It
runs in VBlank because the length of the notes uses the system timers.
Download
RASTER.EXE (Executable program)
Download
/ View
RASTER.LST (Assembler listing)
Download
/ View
RASTER.S (Source file)
SoundSound complements graphics in nearly all arcade-style games.
While most people think of sound effects as the only necessary sound, the
addition of an original background score can contribute greatly to a
game's overall popularity. In either case, the Atari, with its four-voice
sound chip, is well-suited to the task.
The Atari computer has four independent voices that can vary in pitch
by more than three octaves. The tone can vary from very pure to highly
distorted. In addition, each voice has its own loudness level, completely
independent of the television's volume setting.
BASIC's Sound StatmentIn BASIC, the SOUND statement takes the
following form:
SOUND Voice, Pitch, Distortion, Loudness
The first parameter Voice is simple. There are four voices or channels
whose numbers range from 0-3. It takes a separate sound statement to
activate each channel. Initially, at leas tin BASIC, they are all off at
anytime, but anyone can be selectively turned off by setting Pitch,
Distortion, and Loudness for that voice to all zeros.
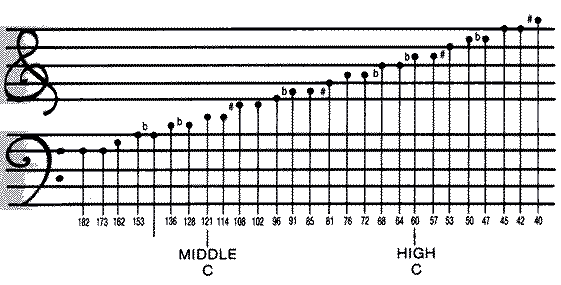
Pitch can vary between 0 -255. The value'N' is used in a divide
circuit. For every N pulses coming in, one pulse goes out. As N gets
larger, the output pulses become less frequent and make a lower note. A
value of 121 produces a middle C tone. A pitch of 60 produces a C tone one
octave higher, and a pitch of 243 produces a C tone one octave lower.
Pitch values around 3 approach the edge of human hearing and may not be
audible on a television speaker that lacks a tweeter.
The Atari computer produces both pure and distorted tones. The term
distortion is actually a misnomer. All of the sound waves on the Atari are
square waves. Distortion doesn't occur because of a degradation of the
wave form like in harmonic audio, but by selectively removing pulses from
the waveform. A more appropriate term would be noise. Distortion values of
10 and 14 generate pure tones. Other even-numbered distortion values
(0,2,4,6, and 12) introduce different amounts of noise into the pure tone.
The quality of the sound depends on both the pitch and the distortion.
Some combinations, mainly distortion 12, combine to produce an undistorted
secondary tone with harmonic overtones.
Loudness is controlled by the fourth number in the SOUND statement. The
value varies from 0 (silent) to 15 (loudest) and is fairly linear for a
single voice. The apparent loudness is affected by pitch. High-pitched
sounds seem quieter than low-pitched sounds. If you are working with
multi-channels, the sum of all four channels should not exceed thirty-two
or it will overmodulate the audio output. The sound produced tends to
actually lose volume and assume a buzzing quality.
Sound DurationSince the SOUND statement lacks a duration
parameter, sound can be turned on and then off by using an empty FOR ...
NEXT loop as a delay. It is largely experimental but empty FOR ... NEXT
loops iterate at approximately 450 times per second. A loop that goes from
1-225 would cause a delay of half a second. Thus, the following three
lines would turn on a tone, let it sound for onehalf second, then turn it
off. 100 SOUND 0,121,10,10
110 FOR I=1 TO 225:NEXT I
120 SOUND 0,0,0,0
Sound EffectsSimple sound effects are created largely by trial
and error. Many use FOR ... NEXT loops to either vary the pitch or vary
the volume. Some do both. The pistol sound in the blocks game in Chapter 5
varies the volume. The bonk sound of the brick being removed is similar
but at another low pitch. Both sounds use distortion or noise to achieve
their effect. 100 REM - PISTOL SOUND
110 FOR L=10 TO 4 STEP -0.25
120 SOUND 0,10,0,L
130 NEXT L
100 REM - BONK SOUND FOR KNOCKING OUT BRICK
110 FOR L=15 TO 0 STEP -0.5
120 SOUND 0,20,2,L
130 NEXT L
It is also possible to vary both the pitch and the volume
simultaneously in a loop. The following example simulates the sound of a
falling bomb. It begins with a high pitch and gradually changes to a low
pitch, followed by the thumping sound of an explosion. 100 REM - FALLING OBJECT
110 FOR L=30 TO 200 STEP 3
120 SOUND 0,L,10,L/25
130 FOR K=1 TO L/10:NEXT K
140 NEXT L
150 SOUND 0,20,0,14
160 SOUND 1,255,10,15
170 FOR K=1 TO 150:NEXT K
180 SOUND 1,0,0,0
Most sound effects have to be placed in a larger loop with the graphics
or player-missile commands, or motion will stop while the sound routine
runs. The problem is that this method often alters the time delays and
preset durations of the sound effects. Worse yet, the location of these
routines within the program changes the result. This occurs because BASIC
must search its line number list whenever it encounters a branch or GOTO
instruction. Obviously, it finds line numbers at the beginning of the
program before it finds line numbers near the end. The only real solution
to the problem is to run your sound routines in the VBlank period, and
this approach requires Machine language programming skills.
Sound-Assembly LanguageThe POKEY digital I/0 chip controls the
audio frequency and the audio control registers for all four sound
channels. The AUDF# (audio frequency) locations are used to control pitch,
and the AUDC# (audio control) locations are used to control distortion and
volume. The sound locations are as follows, and they are write registers
only:
AUDF1 = $D000 AUDC1 = $D001
AUDF2 = $D002 AUDC2 = $D003
AUDF3 =
$D004 AUDC3 = $D005
AUDF4 = 3D006 AUDC4 = $D007
Frequency values range from $00 to $FF. POKEY actually increments this
number by one before sending it to its divide by "N" circuit. For every N
pulses coming in, one pulse comes out. Thus, the higher the value of N,
the lower the tone. The rate of the pulses depends on the POKEY clock.
AUDC1-4 Sound RegistersThe AUDC1-4 locations control both
distortion and volume. The bit pattern is as follows:
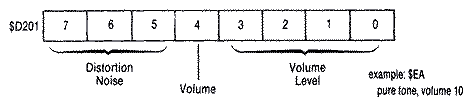
The lower four bits control the volume level (0-15). Zero means no
volume, while 15 means as loud as possible. The only constraint here is
that the total volume for all four sound channels does not exceed
thirty-two. Bit 4 is a volume-only control. Turning this bit on will force
the speaker cone out. Trouble is that this by itself won't produce a tone
since a tone is produced by repeatedly forcing the cone in and out
rapidly. This bit can be useful to advanced sound programmers.
The upper three bits control the distortion. Distortion is produced by
first dividing the clock value by the frequency, then masking the output
using the various poly counters specified by the bit pattern. The result
is finally divided by two. Poly counters or polynomial counters are
actually shift registers that produce various degrees of distortion in
random but repeatable sequences. Since they are repeatable, they are
predictable and are useful for generating sound effects. In general, the
tones become more regular or recognizable with fewer and lower poly
counters masking the output. The 17bit poly counter is useful for white
noise effects like a waterfall, while the 4-bit poly counter is useful for
a motor sound. BIT 7 6 5
0 0 0 5-bit, then 17-bit polys
0 0 1 5-bit poly only
0 1 0 5-bit, then 4-bit polys
0 1 1 5-bit poly only
1 0 0 17-bit poly only
1 0 1 no poly counters (pure tone)
1 1 0 4-bit poly only
1 1 1 oo poly counters (pure tone)
AUDCTL RegisterIn addition to the independent channel control
bytes (AUDC1-4), there is one other register, AUDCTL at 53768 or $D208,
that affects all of the channels. Each bit in AUDCTL is assigned a
specific function. Bit Description
7 Makes the 17-bit poly counter into a 9-bit poly
6 Clock channel one with 1.79 MHz
5 Clock channel three with 1.79 MHz
4 join channels one and two (16 bit)
3 join channels three and four (16 bits)
2 Insert high pass filter into channel one, clocked by
channel two
1 Insert high pass filter into channel two, clocked by
channel four
0 Switch main clock base from 64 KHz to 15 KHz
Shifting the 17-bit poly counters to 9-bit poly counters by setting
bit 7, will create more repeatable sound patterns rather than white
noise-type patterns. Setting the channels to a higher clock frequency
(setting bits 5 and 6), will produce higher tones. Likewise, setting the
bit 7 from 64 KHz to 15 KHz will produce much lower tones.
If you couple two of the sound channels by setting either bits 3 or 4,
you reduce the number of channels to two but gain increased tonal range.
Normally, you get a five octave range using the eight bits of a single
channel, but the combined 16-bit register increases the tonal range to
nine octaves.
Sometimes you may encounter problems POKEing sounds in BASIC or in
Machine language without initializing the sound registers. BASIC requires
a null sound statement, i.e., SOUND 0,0,0,0. In Machine language you need
to store a 0 at AUDCTL ($D208), and a 3 at SKCTL ($D20F).
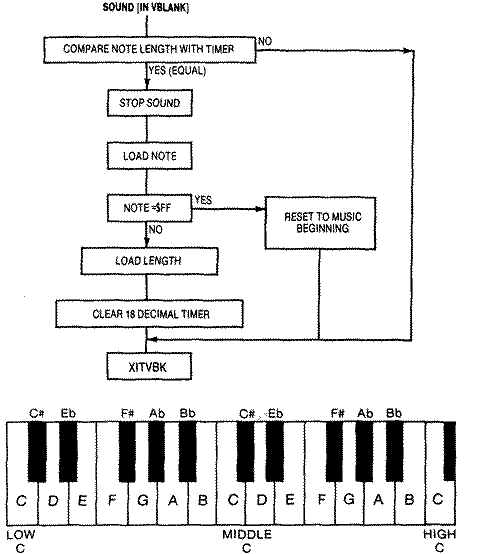
Background MusicOne of the most pleasing uses of sound is to play
musical tunes quietly in the background, during many games or at least use
them to enhance an animated title page. Such routines normally run in the
Vertical Blank period so that the note lengths remain accurate. Generally,
you store the notes and durations of the tune in a table. The Atari reads
the note and its corresponding duration from the table. It then turns on
the note and sustains it until the timer at $14, which counts in jiffies,
reaches the value set by the duration. At that point the note shuts off
and the computer reads the next note and duration. Two consecutive notes
with the same pitch sound like they run together as a much longer note. It
is often necessary to place a zero pitch lasting two jiffies between the
notes. With this method, it is very simple to play an entire musical score
without affecting the play mechanics or speed of a game. Be careful that
you don't use and reset that timer elsewhere in the game.
We use the value of $FF for the note as a flag to indicate the tune is
finished. While it could be used to conclude the piece, we use it to reset
the pointers to the table so that the music repeats endlessly.
The lengths of the different notes is summarized in the table below: NOTE JIFFIES
Sixteenth 8
Eighth 15
Quarter 30
Half 60
Rest 60
(The book indicates a code sample should be inserted here, but it
is missing.)
Sound EffectsExplosion sounds are simple to implement in Machine
language within the Vertical Blank routine. Basically, you need a very
irregular rumbling sound that slowly decreases in volume. Setting the
distortion to zero sets up 17bit poly counters that produce quite
irregular sound. The duration of the sound is controlled by a timer that
counts down every jiffy. This timer can also control the volume level so
that it decreases as a function of the value of the timer. For instance,
if the sound is to take one second, SEXTIME, short for Set Explosion
Timer, is initially set to 64 and is decremented every jiffy. If VOLUME =
SEXTIME / 4, then the volume will decrease from 16 to 0 as SEXTIME counts
down to 0. The code follows: SOUND3 LDA SEXTIME ;CHECK EXPLOSION TIMER FLAG
BEQ .1 ;IF AT 0, NO SOUND
DEC SEXTIME ;COUNTDOWN
LSR ;DIVIDE BY 4 TO GET VOLUME 16-0
LSR
STA AUDC4 ;TELL POKEY NEW SOUND VOLUME
;UPPER NIBBLE (DISTORTION = 0)
LDA #$40 ;TONE
.1 RTS
Laser fire can be simulated by rapidly changing the frequency from a
high pitch to a lower one in discontinuous jumps while using a distortion
set at 6. This produces a more staccato sound than a smooth frequency
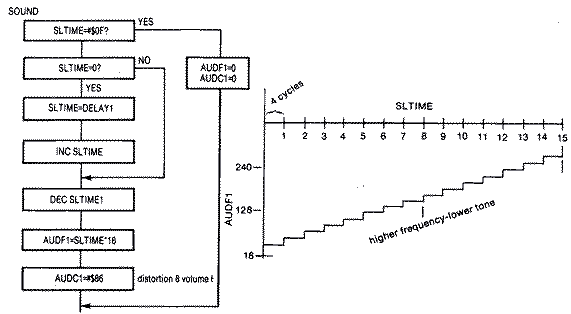
transition. You can implement this effect by making the timer, SLTIME,
short for Set Laser Timer, a function of the frequency. If Frequency =
SLTIME * 16, then each time SLTIME is incremented, the tone will jump in
increments of 16. Remember, the higher the N in the divide by N he lower
the tone. The problem here is that the sound is much too short if to
increment simply from 1 to 15. Therefore, a secondary loop delays each
tonal jump by 4 cycles. The entire sound routine takes 60 jiffies rather
than just 15 jiffies. The flowchart and code are below: SOUND LDA SLTIME ;CHECK LASER TIMER FLAG
BEQ .3 ;IF 0 EXIT
CMP #$0F ;TIMER GOES FROM 1 TO 15
BNE .1
LDA #$00 ;TURN SOUND OFF
STA AUDF1
STA AUDC1
RTS
.1 LDA SLTIME1 ;CHECK DELAY TIMER
BNE .2 ;IF NOT 0 COUNTDOWN TILL IT IS
LDA DELAY1 ;GET NEW DELAY VALUE
STA SLTIME1 ;STORE IT
INC SLTIME ;INCREMENT MAIN TIMER
;(THIS IS ALSO OUR FREQUENCY VALUE)
.2 DEC SLTIME1 ;OUR FREQUENCY VALUE
ASL ;MULTIPLY BY 16
ASL
ASL
ASL
STA AUDFI ;NEW TONE VALUE
LDA #$86 ;DISTORTION 8, VOLUME 6
STA AUDC1
.3 RTS
Return to Table of
Contents | Previous
Chapter | Next Chapter
|
|



